Cho hàm số (y = a{x^3} + b{x^2} + cx + d), với (a,b,c,d) là các số thực và (a)khác 0 (có đồ thị như hình vẽ). Khẳng định nào sau đây sai?

Câu hỏi:

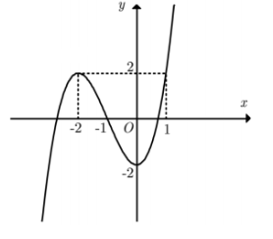
Cho hàm số \(y = a{x^3} + b{x^2} + cx + d\), với \(a,b,c,d\) là các số thực và \(a\)khác 0 (có đồ thị như hình vẽ). Khẳng định nào sau đây sai?

A \(y' < 0,\,\,\forall x \in \left( { - 2;0} \right)\).
B Hàm số đạt GTLN tại điểm \(x = - 2\).
C Đồ thị hàm số có đúng 2 điểm cực trị.
D \(y'(x) = 0 \Leftrightarrow \left[ \begin{array}{l}x = - 2\\x = 0\end{array} \right.\).

Phương pháp giải:

Dựa vào đồ thị hàm số.

Lời giải chi tiết:

Đáp án A đúng. Ta thấy hàm số nghịch biến trên \(\left( {0;2} \right) \Rightarrow y' < 0\,\,\forall x \in \left( {0;2} \right)\).

Đáp án B sai. Hàm số không có GTLN.

Đáp án C đúng. Hàm số có hai điểm cực trị \(x = - 2\) và \(x = 0\).

Đáp án D đúng

Chọn: B

Quảng cáo