Câu hỏi:
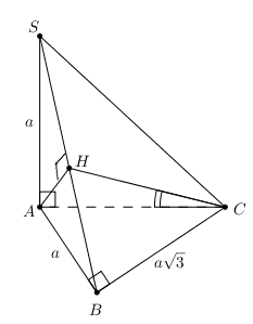
Chóp S.ABC, \(SA\bot \left( ABC \right),\,\,SA=a,\,\,\Delta ABC\) vuông ở B, \(AB=a,\,\,BC=a\sqrt{3}\). Tính \(\widehat{\left( AC;\left( SBC \right) \right)}\) ?
- A \(\arcsin \frac{1}{4}\)
- B \(\arcsin \frac{\sqrt{2}}{4}\)
- C \(\arcsin \frac{1}{\sqrt{3}}\)
- D \(\arcsin \frac{\sqrt{2}}{3}\)
Phương pháp giải:
Lời giải chi tiết:
* Vẽ \(AH\bot SB\Rightarrow AH\bot \left( SBC \right)\Rightarrow \widehat{\left( AC;\left( SBC \right) \right)}=\widehat{\left( AC;HC \right)}=\widehat{ACH}\).
* Chứng minh \(AH\bot \left( SBC \right)\).
* Tính :
+ Tam giác vuông ABC : \(AC=\sqrt{{{a}^{2}}+3{{a}^{2}}}=2a\).
+ \(\frac{1}{A{{H}^{2}}}=\frac{1}{{{a}^{2}}}+\frac{1}{{{a}^{2}}}\Rightarrow AH=\frac{a}{\sqrt{2}}.\)
+ Tam giác vuông AHC: \(\sin \widehat{ACH}=\frac{AH}{AC}=\frac{1}{2\sqrt{2}}=\frac{\sqrt{2}}{4}\) .
Chọn đáp án B.
Quảng cáo
Câu hỏi trước
