Câu hỏi:
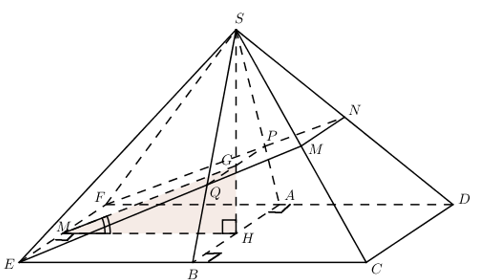
Chóp \(S.ABCD,\,\,\left( SAB \right)\bot \left( ABCD \right),\,\,\Delta SAB\) đều. \(ABCD\) là hình vuông có \(AB=a\). M, N là trung điểm của \(SC,SD\). G là trọng tâm của \(\Delta SAB\). Tính \(\widehat{\left( \left( GMN \right);\left( ABCD \right) \right)}\) .
- A \(\arctan \frac{\sqrt{6}}{6}\)
- B \(\arctan \frac{\sqrt{3}}{6}\)
- C \(\arctan \frac{\sqrt{6}}{3}\)
- D \(\arctan \frac{\sqrt{3}}{3}\)
Phương pháp giải:
Lời giải chi tiết:
* Vẽ \(SH\bot AB\Rightarrow SH\bot \left( ABCD \right)\). H là trung điểm của AB.
Vẽ \(G\in SH\) để \(\frac{SG}{SH}=\frac{2}{3}\Rightarrow G\) là trọng tâm \(\Delta SAB\).
* Qua G vẽ \(PQ//AB\,\,\left( P\in SA;Q\in SB \right)\Rightarrow PQ//MN\)
\(\Rightarrow \left( GMN \right)\equiv \left( MNPQ \right)\)
* Nối \(MQ\cap BC=E;\,\,NP\cap AD=F\)
\(\Rightarrow \left( MNPQ \right)\cap \left( ABCD \right)=EF\)
* Nhận xét : Xác định góc bằng trường hợp 3.
* Bước 1 : Chọn \(G\in \left( MNPQ \right).\) Ta có : \(GH\bot \left( ABCD \right)\) , vẽ \(HM\bot EF\)
\(\Rightarrow \widehat{\left( \left( MNPQ \right);\left( ABCD \right) \right)}=\widehat{GMH}\)
* Bước 2 : Tính.
Nhận xét : \(\Delta SFD\) có :
FN là trung tuyến.
\(P\in SA\) để \(\frac{SP}{SA}=\frac{2}{3}\)
\(\Rightarrow P\) là trọng tâm \(\Delta SFD\Rightarrow \)A là trung điểm của FD.
\(\Rightarrow FA=a=MH\).
Có \(GH=\frac{1}{3}SH=\frac{a\sqrt{3}}{6}\)
\(\Delta GMH\) có \(\tan \widehat{GMH}=\frac{GH}{MH}=\frac{\sqrt{3}}{6}\)
Đáp số: \(\arctan \frac{\sqrt{3}}{6}\)