Câu hỏi:
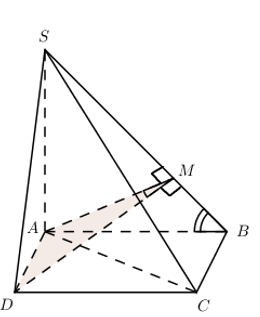
Chóp \(S.ABCD\), \(SA\bot \left( ABCD \right)\). \(SA=a\), \(ABCD\) là hình vuông có \(AB=a\).
a) Tính \(\widehat{\left( \left( SBC \right);\left( ABCD \right) \right)}\) .
b) Tính \(\widehat{\left( \left( SBD \right);\left( SAB \right) \right)}\).
c) Tính \(\widehat{\left( \left( SAD \right);\left( SBC \right) \right)}\). .
- A a) \({{45}^{0}}\).
b) \(\arctan \sqrt{2}\).
c) \({{45}^{0}}\)
- B a) \(\arctan \sqrt{2}\).
b) \({{45}^{0}}\).
c) \({{45}^{0}}\)
- C a) \({{45}^{0}}\)
b) \({{45}^{0}}\).
c) \(\arctan \sqrt{2}\).
- D a) \({{45}^{0}}\)
b) \({{45}^{0}}\).
c) \({{45}^{0}}\).
Phương pháp giải:
Lời giải chi tiết:
a) Tính \(\widehat{\left( \left( SBC \right);\left( ABCD \right) \right)}\). (Trường hợp 3).
* Bước 1: Chọn S. Ta có: \(\left\{ \begin{align} SB\bot BC \\ AB\bot BC \\ \end{align} \right.\)
\(\Rightarrow \widehat{\left( \left( SBC \right);\left( ABCD \right) \right)}=\widehat{SBA}\)
* Bước 2 : \(\Delta SAB\) vuông cân tại A \(\Rightarrow \widehat{SBA}={{45}^{0}}\)
Đáp số: \({{45}^{0}}\).
b) Tính \(\widehat{\left( \left( SBD \right);\left( SAB \right) \right)}\).
* Nhận xét: Dùng trường hợp 3 để giải.
* Bước 1: Chọn \(D\in \left( SBD \right)\). Ta có: \(DA\bot \left( SAB \right)\) , vẽ \(AM\bot SB\).
\(\Rightarrow \widehat{\left( \left( SBD \right);\left( SAB \right) \right)}=\widehat{DMA}\)
Đáp số: \(\arctan \sqrt{2}\).
* Bước 2 : Tính
\(\Delta SAB\) có : \(\frac{1}{A{{M}^{2}}}=\frac{1}{{{a}^{2}}}+\frac{1}{{{a}^{2}}}\Rightarrow AM=\frac{a}{\sqrt{2}}\)
\(\Delta MAD\) có : \(\tan \widehat{DMA}=\frac{AD}{AM}=a:\frac{a}{\sqrt{2}}=\sqrt{2}\)
\(\Rightarrow \widehat{\left( \left( SBD \right);\left( SAB \right) \right)}=\arctan \sqrt{2}\)
c) Nhận xét : Sử dụng cá biệt loại 2 vì AD // BC.
* Bước 1 : Ta có \(SA\bot AD\) và \(SB\bot BC\)
\(\Rightarrow \widehat{\left( \left( SAD \right);\left( SBC \right) \right)}=\widehat{\left( SA;SB \right)}=\widehat{SAB}\)
* Bước 2 : Tính
\(\Delta ASB\) vuông cân ở A \(\Rightarrow \widehat{ASB}={{45}^{0}}\)
Đáp số: \({{45}^{0}}\)