Câu hỏi:
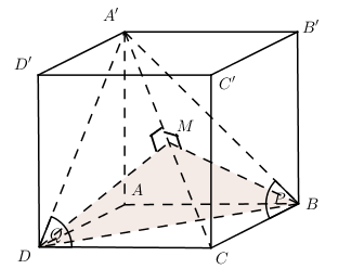
Hình lập phương \(ABCD.A'B'C'D'\), \(AB=a\). Tính \(\widehat{\left( \left( A'BC \right);\left( A'CD \right) \right)}\).
- A \({{45}^{0}}\)
- B \({{90}^{0}}\)
- C \({{30}^{0}}\)
- D \({{60}^{0}}\)
Phương pháp giải:
Lời giải chi tiết:
* Nhận xét: \(\Delta A'BC=\Delta A'DC\)
* Bước 1: Vẽ \(DM\bot A'C\Rightarrow \widehat{\left( \left( A'BC \right);\left( A'CD \right) \right)}=\widehat{DMB}\)
* Bước 2: \(CB\bot AB\Rightarrow CB\bot A'B\)
Tính \(\frac{1}{B{{M}^{2}}}=\frac{1}{{{a}^{2}}}+\frac{1}{2{{a}^{2}}}\Rightarrow B{{M}^{2}}=\frac{2{{a}^{2}}}{3}\)
\(\begin{align} \cos M=\frac{B{{D}^{2}}-M{{B}^{2}}-M{{D}^{2}}}{-2MB.MD}=-\frac{1}{2} \\ \Rightarrow \widehat{DMB}={{120}^{0}}\Rightarrow \widehat{\left( \left( A'BC \right);\left( A'CD \right) \right)}={{60}^{0}} \\ \end{align}\)
Đáp số: \({{60}^{0}}\)
Quảng cáo