Câu hỏi:
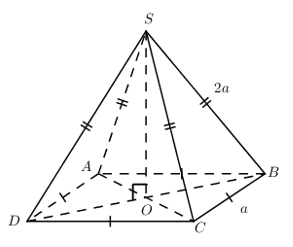
Cho hình chóp đều S.ABCD, \(SA=2a;\,\,AB=a\). Tính \(d\left( S;\left( ABCD \right) \right)\).
- A \(\frac{a\sqrt{11}}{2}\)
- B \(\frac{a\sqrt{12}}{2}\)
- C \(\frac{a\sqrt{13}}{2}\)
- D \(\frac{a\sqrt{14}}{2}\)
Phương pháp giải:
Lời giải chi tiết:
* Nối \(AC\cap BD=O\Rightarrow O\) là tâm đáy \(\Rightarrow SO\bot \left( ABCD \right)\).
\(\Rightarrow d\left( S;\left( ABCD \right) \right)=SO\).
* Tính SO : \(BD=a\sqrt{2}\Rightarrow OB=\frac{a\sqrt{2}}{2}\)
\({{\Delta }_{v}}SOB:\,\,SO=\sqrt{S{{B}^{2}}-O{{B}^{2}}}=\sqrt{4{{a}^{2}}-\frac{2{{a}^{2}}}{4}}=\frac{a\sqrt{14}}{2}\)
Chọn đáp án D.
Quảng cáo