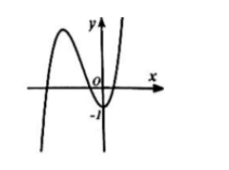
Câu hỏi:
Đường cong bên là đồ thị của một trong bốn hàm số đã cho sau đây. Hỏi đó là hàm số nào?
- A
\(y={{x}^{3}}+3{{x}^{2}}-1\)
- B
\(y={{x}^{4}}+{{x}^{2}}-1\)
- C
\(y={{x}^{3}}-3x-1\)
- D \(y=-{{x}^{2}}-3x-1\)
Phương pháp giải:
Đồ thị có hình dáng hàm đa thức bậc ba \(y=a{{x}^{3}}+b{{x}^{2}}+cx+d\)
Dựa vào \(\underset{x\to -\infty }{\mathop{\lim }}\,y\Rightarrow \) dấu của a.
Dựa vào giao điểm của đồ thị hàm số với trục tung \(\Rightarrow c\).
Dựa vào số điểm cực trị suy ra đáp án.
Lời giải chi tiết:
Đồ thị có hình dáng hàm đa thức bậc ba \(y=a{{x}^{3}}+b{{x}^{2}}+cx+d\Rightarrow \)Loại B và D.
Đáp án A: \(y'=3{{x}^{2}}+6x=0\Rightarrow \left[ \begin{align} x=0 \\ x=-2 \\ \end{align} \right.\)
Đáp án C: \(y'=3{{x}^{2}}-3=0\Leftrightarrow \left[ \begin{align} x=1 \\ x=-1 \\ \end{align} \right.\).
Dựa vào đồ thị hàm số ta thấy hàm số đạt cực tiểu tại x = 0 \(\Rightarrow \) Loại đáp án C.
Chọn A.