Câu hỏi:
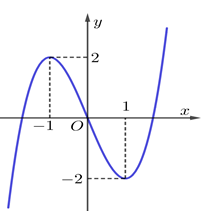
Đường cong trong hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào ?
- A \(y={{x}^{3}}-3x.\)
- B \(y=-\,{{x}^{3}}+3x.\)
- C \(y={{x}^{4}}-2{{x}^{2}}.\)
- D \(y={{x}^{3}}-{{x}^{2}}.\)
Phương pháp giải:
Dựa vào hình dáng của đồ thị hàm số, điểm cực trị và tọa độ giao điểm với hai trục tọa độ
Lời giải chi tiết:
Dựa vào hình vẽ, ta thấy rằng:
• Đồ thị hàm số bậc ba, có \(\underset{x\,\to \,+\,\infty }{\mathop{\lim }}\,f\left( x \right)=+\,\infty \)\(\Rightarrow \) Hệ số \(a>0.\)
• Đồ thị nhận gốc tọa độ \(O\left( 0;0 \right)\) làm tâm đối xứng \(\Rightarrow \) Hàm lẻ: \(f\left( x \right)=f\left( -\,x \right)\)
Trong 4 đáp án, có duy nhất hàm số \(y={{x}^{3}}-3x\) thỏa mãn 2 điều kiện trên.
Chọn A
Quảng cáo