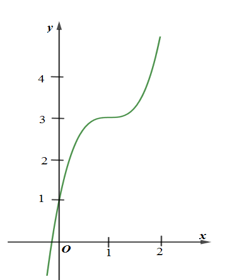
Câu hỏi:
Đường cong ở hình bên là đồ thị của một trong bốn hàm số ở dưới đây. Hàm số đó là hàm số nào?
- A \(y=-2{{x}^{3}}-6{{x}^{2}}+6x+1\).
- B \(y=2{{x}^{3}}-6{{x}^{2}}+6x+1\).
- C \(y=-2{{x}^{3}}-6{{x}^{2}}-6x+1\).
- D \(y=2{{x}^{3}}-6{{x}^{2}}-6x+1\).
Phương pháp giải:
- Loại trừ phương án sai.
Lời giải chi tiết:
Hàm số ở bốn phương án có dạng \(y=a{{x}^{3}}+b{{x}^{2}}+cx+d,\,\,a\ne 0\).
Quan sát đồ thị hàm số ta thấy hàm số đồng biến trên R \(\Rightarrow a>0\)
\(\Rightarrow \)Loại đi phương án A và C.
Mặt khác, hàm số đồng biến trên R \(\Rightarrow y'\ge 0,\,\,\forall x\)
Xét \(y=2{{x}^{3}}-6{{x}^{2}}-6x+1\Rightarrow y'=6{{x}^{2}}-12x-6\)
\(y'=0\)có hai nghiệm phân biệt \(\Rightarrow \) \(y=2{{x}^{3}}-6{{x}^{2}}-6x+1\) có khoảng đồng biến, có khoảng nghịch biến.
\(\Rightarrow \) Loại đi phương án D.
\(\Rightarrow \) Chọn phương án B.
Chọn: B
Quảng cáo