Phương pháp giải:

Tính thể tích ${{V}_{S.ABC}}=\frac{1}{3}SA.{{S}_{ABC}}$ theo $\cos \alpha$.

Lời giải chi tiết:

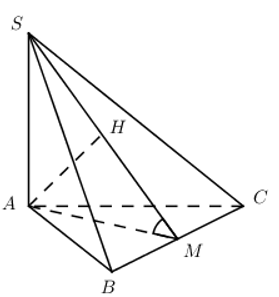
Gọi M là trung điểm của BC ta có: $\left\{ \begin{align}  & BC\bot AM \\  & BC\bot SA \\ \end{align} \right.\Rightarrow BC\bot \left( SAM \right)$

Trong (SAM) kẻ $AH\bot SM\Rightarrow AH\bot BC\Rightarrow AH\bot \left( SBC \right)\Rightarrow AH=3$

Ta có :

$\left\{ \begin{align} & \left( SBC \right)\cap \left( ABC \right)=BC \\ & AM\bot BC \\  & SM\bot BC \\ \end{align} \right.\Rightarrow \widehat{\left( \left( SBC \right);\left( ABC \right) \right)}=\widehat{\left( AM;SM \right)}=\widehat{SMA}=\alpha$

$\Rightarrow AM=\frac{AH}{\sin \alpha }=\frac{3}{\sin \alpha }\Rightarrow BC=2AM=\frac{6}{\sin \alpha }$

$\Rightarrow {{S}_{ABC}}=\frac{1}{2}AM.BC=\frac{1}{2}.\frac{3}{\sin \alpha }.\frac{6}{\sin \alpha }=\frac{9}{{{\sin }^{2}}\alpha }$ 

Trong tam giác vuông SAM có: $SM=\frac{AM}{\cos \alpha }=\frac{3}{\sin \alpha \cos \alpha }$

$\begin{align}  & \Rightarrow SA=\sqrt{S{{M}^{2}}-A{{M}^{2}}}=\sqrt{\frac{9}{{{\sin }^{2}}\alpha {{\cos }^{2}}\alpha }-\frac{9}{{{\sin }^{2}}\alpha }}=\frac{3\sqrt{1-{{\cos }^{2}}\alpha }}{\sin \alpha \cos \alpha }=\frac{3}{\cos \alpha } \\  & \Rightarrow {{V}_{S.ABC}}=\frac{1}{3}SA.{{S}_{ABC}}=\frac{1}{3}\frac{3}{\cos \alpha }.\frac{9}{{{\sin }^{2}}\alpha }=\frac{9}{\left( 1-{{\cos }^{2}}\alpha  \right)\cos \alpha } \\ \end{align}$

Đặt $t=\cos \alpha \,\,\left( 0<t<1 \right)\Rightarrow f\left( t \right)=\frac{9}{\left( 1-{{t}^{2}} \right)t}$

$\begin{align}  & f\left( \frac{1}{3} \right)=\frac{243}{8};\,\,f\left( \frac{\sqrt{3}}{3} \right)=\frac{27\sqrt{3}}{2};\,\,f\left( \frac{\sqrt{2}}{2} \right)=18\sqrt{2};\,\,f\left( \frac{2}{3} \right)=\frac{243}{10} \\  & \Rightarrow \underset{x\in \left( 0;1 \right)}{\mathop{\min }}\,f\left( t \right)=f\left( \frac{\sqrt{3}}{3} \right) \\ \end{align}$

Chọn B.