Câu hỏi:
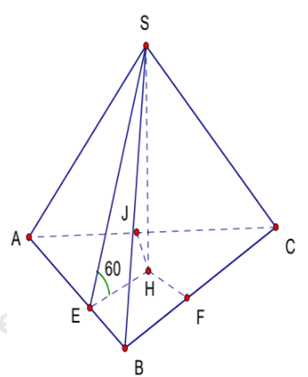
Cho hình chóp \(S.ABC\) có \(AB=5a,\,\,BC=6a,\,\,CA=7a.\) Các mặt bên \(\left( SAB \right)\) và \(\left( SBC \right),\) \(\left( SCA \right)\) tạo với đáy một góc \({{60}^{0}}.\) Tính thể tích khối chóp \(S.ABC.\)
- A \(\frac{{{a}^{3}}\sqrt{3}}{2}.\) .
- B \(8{{a}^{3}}\sqrt{3}.\)
- C \(\frac{8{{a}^{3}}\sqrt{3}}{3}.\)
- D \(4{{a}^{3}}\sqrt{3}.\)
Phương pháp giải:
Xác định chân đường cao kẻ từ đỉnh của hình chóp bằng dữ liệu góc, từ đó suy ra độ dài đường cao của khối chóp và tính thể tích
Lời giải chi tiết:
Gọi \(H\) là hình chiếu vuông góc của \(S\) trên mặt phẳng \(\left( ABC \right).\)
Gọi \(E,\,\,F,\,\,J\) lần lượt là hình chiếu của \(H\) trên \(AB,\,\,BC,\,\,CA.\)
Khi đó \(\widehat{SEH}=\widehat{SFH}=\widehat{SJH}={{60}^{0}}\)\(\Rightarrow \,\,HE=HF=HJ\)
\(\Rightarrow \,\,H\) là tâm đường tròn nội tiếp \(\Delta \,ABC.\)
Diện tích tam giác \(ABC\) là \(S=\sqrt{p\left( p-a \right)\left( p-b \right)\left( p-c \right)}=6a\sqrt{6}.\)
Bán kính đường tròn nội tiếp \(\Delta \,ABC\) là \(EH=r=\frac{S}{p}=\frac{2a\sqrt{6}}{3}.\)
Tam giác \(SEH\) vuông tại \(H,\) có \(\tan \widehat{SEH}=\frac{SH}{EH}\Rightarrow SH=2a\sqrt{2}.\)
Vậy thể tích khối chóp \(S.ABC\) là \({{V}_{S.ABC}}=\frac{1}{3}.SH.{{S}_{\Delta \,ABC}}=\frac{1}{3}.2a\sqrt{2}.6a\sqrt{6}=8{{a}^{3}}\sqrt{3}.\)
Chọn B