Câu hỏi:
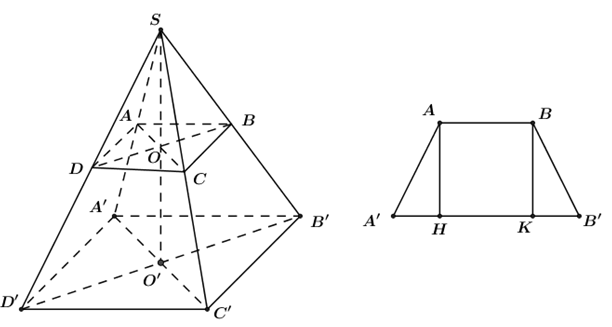
Cho hình chóp cụt tứ giác đều \(ABCD.{A}'{B}'{C}'{D}'\) có chiều cao bằng \(a\sqrt{2}\) và \({A}'{B}'=2\,AB=2a.\) Tính diện tích xung quanh của hình chóp cụt đều đó.
- A \(9{{a}^{2}}.\)
- B \(\frac{9{{a}^{2}}}{4}.\)
- C \(14{{a}^{2}}.\)
- D \(3\sqrt{3}\,{{a}^{2}}.\)
Phương pháp giải:
Vẽ hình, tính toán xác định diện tích các mặt xung quanh của hình chóp cụt tứ giác đều.
Lời giải chi tiết:
Diện tích hình vuông \(ABCD\) là \({{S}_{ABCD}}=A{{B}^{2}}={{a}^{2}}.\)
Diện tích hình vuông \({A}'{B}'{C}'{D}'\) là \({{S}_{{A}'{B}'{C}'{D}'}}=A'B{{'}^{2}}=4{{a}^{2}}.\)
Các mặt bên của hình chóp cụt \(ABCD.{A}'{B}'{C}'{D}'\) là các hình thang cân có diện tích bằng nhau.
Gọi \(O,\,\,{O}'\) lần lượt là tâm của hình vuông \(ABCD,\,\,{A}'{B}'{C}'{D}'\)
Nối \(O{O}'\) cắt \(A{A}'\) tại \(S,\) khi đó \(S{A}'=\sqrt{S{{{{O}'}}^{2}}+{O}'{{{{A}'}}^{2}}}=\sqrt{{{\left( 2a\sqrt{2} \right)}^{2}}+{{\left( a\sqrt{2} \right)}^{2}}}=a\sqrt{10}.\)
Suy ra \(A{A}'=\frac{S{A}'}{2}=\frac{a\sqrt{10}}{2}\).
Xét hình thang ABA’B’ ta có : \(A'H=\frac{A'B'-AB}{2}=\frac{2a-a}{2}=\frac{a}{2}.\)
\(\Rightarrow AH=\sqrt{AA{{'}^{2}}-A'H}=\sqrt{\frac{10{{a}^{2}}}{4}-\frac{{{a}^{2}}}{4}}=\frac{3a}{2}.\)
Diện tích hình thang cân \(A{A}'{B}'B\) là : \(S={{S}_{AA'B'B}}=\frac{AB+A'B'}{2}.AH=\frac{2a+a}{2}.\frac{3a}{2}=\frac{9{{a}^{2}}}{4}.\)
Vậy diện tích xung quanh của hình chóp cụt là\({S_{xq}} = S _{ABCD} + {S_{A'B'C'D'}} + 4.S = {a^2} + 4{a^2} + 4.\frac{{9{a^2}}}{4} = 14{a^2}.\)
Chọn C