Câu hỏi:
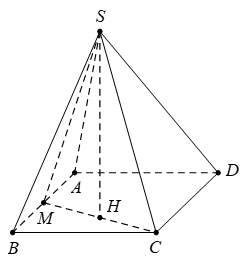
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình chữ nhật, \(AB=2a,\,\,AD=a.\) Gọi \(M\) là trung điểm của \(AB,\,\,\,\Delta \,SMC\) vuông tại \(S,\,\,\,\left( SMC \right)\bot \left( ABCD \right).\) Đường thẳng \(SM\) tạo với đáy góc \({{60}^{0}}.\) Thể tích của khối chóp \(S.ABCD\) bằng
- A \(\frac{{{a}^{3}}\sqrt{3}}{6}.\)
- B \(\frac{{{a}^{3}}}{3}.\)
- C \(\frac{2{{a}^{3}}\sqrt{6}}{3}.\)
- D \(\frac{{{a}^{3}}\sqrt{6}}{6}.\)
Phương pháp giải:
Dựa vào dữ kiện góc và mặt phẳng vuông góc với hai mặt phẳng để xác định chiều cao khối chóp.
Lời giải chi tiết:
Gọi \(H\) là hình chiếu của \(S\) trên \(MC\)\(\Rightarrow \,\,SH\bot \left( ABCD \right).\)
Ta có \(\widehat{SM;\left( ABCD \right)}=\widehat{\left( SM;MH \right)}=\widehat{SMH}={{60}^{0}}.\)
Tam giác \(BMC\) vuông tại \(B,\) có \(MC=\sqrt{B{{M}^{2}}+B{{C}^{2}}}=a\sqrt{2}.\)
Tam giác \(SMC\) vuông tại \(S,\) có
\(\cos \widehat{SMC}=\frac{SM}{MC}\Rightarrow SM=\cos {{60}^{0}}.a\sqrt{2}=\frac{a\sqrt{2}}{2}\Rightarrow SC=\frac{a\sqrt{6}}{2}.\)
Suy ra \(SH=\frac{SM.SC}{MC}=\left( \frac{a\sqrt{2}}{2}.\frac{a\sqrt{6}}{2} \right):a\sqrt{2}=\frac{a\sqrt{6}}{4}.\)
Vậy thể tích khối chóp \(S.ABCD\) là \(V=\frac{1}{3}.SH.{{S}_{ABCD}}=\frac{1}{3}.\frac{a\sqrt{6}}{4}.2{{a}^{2}}=\frac{{{a}^{3}}\sqrt{6}}{6}.\)
Chọn D