Câu hỏi:
Cho hình chóp S.ABC có SA = SB = SC = 2a và tam giác ABC có góc A bằng \({{120}^{0}}\) và \(BC=2a\). Tính bán kính mặt cầu ngoại tiếp hình chóp theo \(a\)
- A \(\frac{a\sqrt{3}}{2}\).
- B \(\frac{2a\sqrt{3}}{3}\).
- C \(\frac{a\sqrt{6}}{6}\).
- D \(\frac{a\sqrt{6}}{2}\).
Phương pháp giải:
- Xác định chính xác vị trí của tâm mặt cầu.
- Sử dụng định lý Sin, tính bán kính đường tròn ngoại tiếp tam giác đáy
\(\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}=2R\)
Trong đó, R: bán kính đường tròn ngoại tiếp tam giác ABC.
Lời giải chi tiết:
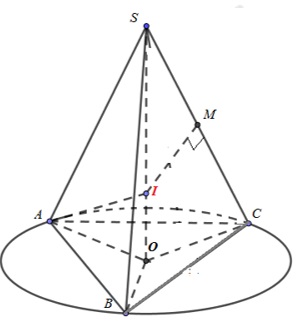
Vì SA = SB = SC nên hình chiếu của S lên mặt phẳng (ABC) là tâm đường tròn ngoại tiếp tam giác ABC.
Gọi O là tâm đường tròn ngoại tiếp tam giác \(ABC\Rightarrow SO\bot (ABC)\).
Gọi M là trung điểm của SC.
Trong mặt phẳng (SOC), dựng \(MI\bot SC,\,\,I\in SO\).
Vì \(I\in SO\Rightarrow IA=IB=IC\)
\(I\in IM\Rightarrow IS=IC\)
\(\Rightarrow IA=IB=IC=IS\Rightarrow \) I là tâm mặt cầu ngoại tiếp hình chóp S.ABC.
Áp dụng định lý Sin, ta có : \(\frac{BC}{\sin A}=2r\) (r: bán kính đường tròn ngoại tiếp tam giác ABC)
\(\Leftrightarrow \frac{2a}{\sin {{120}^{0}}}=2r\Leftrightarrow r=\frac{2a}{\sqrt{3}}\)
Tam giác SOC vuông tại O: \(S{{O}^{2}}=S{{C}^{2}}-O{{C}^{2}}={{(2a)}^{2}}-{{\left( \frac{2a}{\sqrt{3}} \right)}^{2}}=\frac{8a}{3}\Rightarrow SO=a\sqrt{\frac{8}{3}}\).
Dễ dàng chứng minh: \(\Delta SMI\) đồng dạng \(\Delta SOC\Rightarrow \frac{SI}{SC}=\frac{SM}{SO}\Leftrightarrow \frac{SI}{2a}=\frac{a}{a\sqrt{\frac{8}{3}}}\Rightarrow SI=\frac{a\sqrt{6}}{2}\)
Vậy, bán kính mặt cầu ngoại tiếp hình chóp S.ABC bằng \(SI=\frac{a\sqrt{6}}{2}\).
Chọn: D.


















