Câu hỏi:
Cho đồ thị hàm số \(y=f\left( x \right)\) như hình vẽ. Mệnh đề nào sau đây sai?
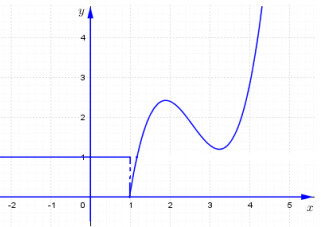
- A Hàm số có tại hàm tại x = 0
- B Hàm số có tại hàm tại x = 1
- C Hàm số có tại hàm tại x = 2
- D Hàm số có tại hàm tại x = 3
Phương pháp giải:
Đạo hàm của hàm số \(y=f\left( x \right)\) tại điểm \(x={{x}_{0}}\) là \(f'\left( {{x}_{0}} \right)=\underset{x\to {{x}_{0}}}{\mathop{\lim }}\,\frac{f\left( x \right)-f\left( {{x}_{0}} \right)}{x-{{x}_{0}}}\) (nếu tồn tại).
Lời giải chi tiết:
Dựa vào đồ thị hàm số ta thấy \(\underset{x\to {{1}^{-}}}{\mathop{\lim }}\,f\left( x \right)=1,\,\,\underset{x\to {{1}^{+}}}{\mathop{\lim }}\,f\left( x \right)=0\Rightarrow \underset{x\to {{1}^{-}}}{\mathop{\lim }}\,f\left( x \right)\ne \underset{x\to {{1}^{+}}}{\mathop{\lim }}\,f\left( x \right)\Rightarrow \) Không tồn tại \(\underset{x\to 1}{\mathop{\lim }}\,f\left( x \right)\), hàm số không liên tục tại x = 1.
Vậy hàm số không có tại hàm tại x = 1
Chọn B.


















