Câu hỏi:
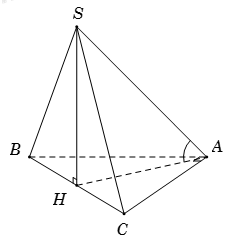
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A, \(\widehat {ABC} = {60^0}\), tam giác SBC là tam giác đều có cạnh bằng 2a và hình chiếu vuông góc của S trên mặt phẳng (ABC) trùng với trung điểm của BC. Tính góc giữa đường thẳng SA và mặt phẳng đáy (ABC).
- A \({30^0}.\)
- B \({45^0}.\)
- C \({60^0}.\)
- D \({90^0}.\)
Phương pháp giải:
Áp dụng phương pháp tìm góc giữa đường thẳng và mặt phẳng – hệ thức lượng trong tam giác vuông để giải quyết yêu cầu của bài toán
Lời giải chi tiết:
Gọi H là trung điểm của BC, suy ra \(SH \bot \left( {ABC} \right)\).
Vì \(SH \bot \left( {ABC} \right)\) nên HA là hình chiếu của SA trên mp(ABC).
Do đó \(\widehat {\left( {SA;\left( {ABC} \right)} \right)} = \widehat {\left( {SA;AH} \right)} = \widehat {SAH}\).
● Tam giác SBC đều cạnh 2a nên \(SH = \frac{{2a\sqrt 3 }}{2} = a\sqrt 3 .\)
● Tam giác ABC vuông tại A nên \(AH = \frac{1}{2}BC = a.\)
Tam giác vuông SAH, có \(\tan \widehat {SAH} = \frac{{SH}}{{AH}} = \sqrt 3 \)\( \Rightarrow \widehat {SAH} = {60^0}\).
Chọn C.