Phương pháp giải:

Sử dụng lý thuyết của đường thẳng vuông góc với mặt phẳng

Lời giải chi tiết:

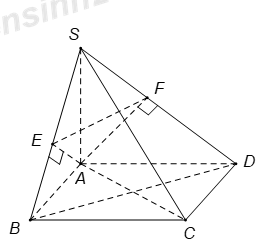
Vì SA vuông góc với mặt phẳng (ABCD)$\Rightarrow$$SA\bot BC.$

Mà $AB\bot BC$ nên suy ra $BC\bot \left( SAB \right)\Rightarrow BC\bot AE\subset \left( SAB \right).$

Tam giác SAB có đường cao AE$\Rightarrow \,\,AE\bot SB$

Mà $AE\bot BC\Rightarrow AE\bot \left( SBC \right)\Rightarrow AE\bot SC.$

Tương tự, ta chứng minh được $AF\bot SC$. Do đó $SC\bot \left( AEF \right).$

Chọn D