Câu hỏi:
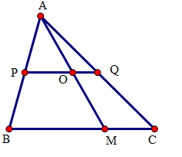
Cho tam giác \(ABC\), khi điểm \(M\) di chuyển trên cạnh \(BC\) thì trung điểm \(O\) của đoạn thẳng \(AM\) di chuyển trên
- A Đường thẳng \(a\) song song với cạnh \(AB\)
- B Đường cao của tam giác \(ABC\)
- C Đường thẳng \(a\) song song với cạnh \(BC\), cách \(BC\) một khoẳng bằng \(\frac{{AM}}{2}\)
- D Đường thẳng \(PQ\) song song với cạnh \(BC\), với \(P, Q\) là trung điểm của các cạnh \(AB, AC\)
Phương pháp giải:
+ Chứng minh \(PQ\) là đường trung bình của tam giác \(ABC\) để suy ra \(PQ // BC\).
+ Chứng minh \(O\) thuộc \(PQ\)
Lời giải chi tiết:
Gọi \(P, Q\) lần lượt là trung điểm của \(AB, AC\). Suy ra \(PQ\) là đường trung bình của tam giác \(ABC\). Do đó \(PQ // BC\)
Nếu \(M\) trùng với \(B\) thì ta có \(O\) trùng với \(P\)
Nếu \(M\) trùng với \(C\) thì \(O\) trùng với \(Q\).
Do đó nếu \(M\) di chuyển trên \(BC\) thì \(O\) di chuyển trên đường thẳng \(PQ\) song song với cạnh \(BC\), với \(P, Q\) là trung điểm của các cạnh \(AB, AC\)
Chọn D
Quảng cáo