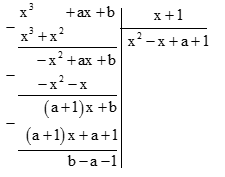Câu hỏi:
Tìm các hằng số a và b sao cho \(\left( {{x^3} + ax + b} \right):\left( {x + 1} \right)\) dư 7 và \(\left( {{x^3} + ax + b} \right):\left( {x - 3} \right)\) dư (- 5)
- A a = -10; b = 2
- B a = -10; b = - 2
- C a = 10; b = 2
- D a = -10; b = 3
Phương pháp giải:
- Đặt phép chia.
- Để phép chia có dư theo điều kiện đề bài thì số dư cuối cùng phải bằng số dư đề bài cho. Từ đó ta được phương trình thứ nhất.
- Thực hiện tương tự, được phương trình thứ hai. Lập hệ phương trình, giải hệ thu được giá trị của a và b.
Lời giải chi tiết:
Để \({x^3} + ax + b\) chia cho x + 1 dư 7 thì \(b - a - 1 = 7 \Leftrightarrow - a + b = 8\;(1)\)
Để \({x^3} + ax + b\) chia cho x - 3 dư - 5 thì \(b + 3a + 27 = -5 \Leftrightarrow 3a + b = - 32\;(2)\)
Từ (1) và (2) ta có hệ \(\left\{ \matrix{- a + b = 8 \hfill \cr 3a + b = - 32 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{a = - 10 \hfill \cr b = - 2 \hfill \cr} \right.\)
Câu hỏi trước
