Câu hỏi:
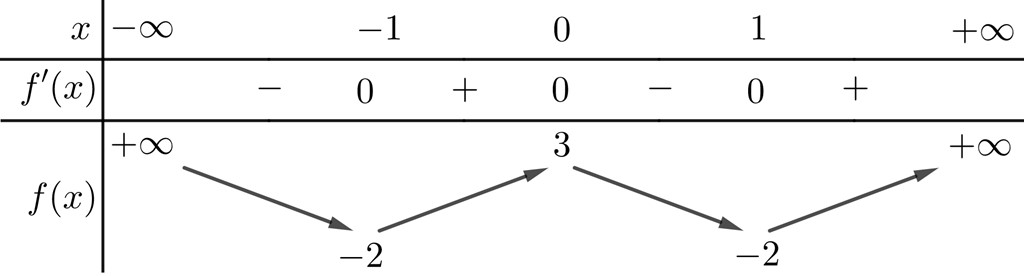
Cho hàm số \(y = {\rm{ }}f\left( x \right)\) có bảng biến thiên dưới đây. Khẳng định nào sau đây là đúng?
- A
Hàm số y = f(x) đồng biến trên \(\left( { - \infty \,;\; - 1} \right)\)
- B
Hàm số y = f(x) nghịch biến trên \(\left( {\,1\;;\, + \infty } \right)\)
- C
Hàm số y = f(x) đồng biến trên \(\left( { - 1\,;\;1} \right)\)
- D
Hàm số y = f(x) nghịch biến trên \(\left( {0\,;\;1} \right)\)
Phương pháp giải:
Quan sát hướng các mũi tên (từ trái qua phải) trong bảng biến thiên:
+ Mũi tên đi lên tức là hàm số đồng biến trên khoảng đó.
+ Mũi tên đi xuống tức là hàm số nghịch biến trên khoảng đó.
Lời giải chi tiết:
Các khoảng đồng biến của hàm số là: \(\left( { - 1\,;\;0} \right)\) và \(\left( {\,1\;;\, + \infty } \right)\)
Các khoảng nghịch biến của hàm số là: \(\left( { - \infty \,;\; - 1} \right)\) và \(\left( {0\,;\;1} \right)\)
Câu hỏi trước
