Phương pháp giải:

+ Sử dụng phương pháp tích phân từng phần u=x,v=f(x).

+ Đổi biến số $t = \frac{\pi }{2} - x$

+ Sử dụng tính chất $\int\limits_a^b {f\left( x \right)dx}  = \int\limits_a^b {f\left( t \right)dt}$.

Lời giải chi tiết:

$\begin{array}{l}I = \int\limits_0^{\frac{\pi }{2}} {xf'\left( x \right)dx}  = \int\limits_0^{\frac{\pi }{2}} {xd\left[ {f\left( x \right)} \right]} \\ = x.f\left( x \right) - \int\limits_0^{\frac{\pi }{2}} {f\left( x \right)dx}  =  - \int\limits_0^{\frac{\pi }{2}} {f\left( x \right)dx} \end{array}$

Ta có $f\left( x \right) + f\left( {\frac{\pi }{2} - x} \right) = \sin x.\cos x$ nên

$f\left( x \right) = \sin x.\cos x - f\left( {\frac{\pi }{2} - x} \right)$ thay vào I ta được:

$I = \int\limits_0^{\frac{\pi }{2}} {\left[ {f\left( {\frac{\pi }{2} - x} \right) - \sin x.\cos x} \right]dx}$

Đặt $t = \frac{\pi }{2} - x \Rightarrow x = \frac{\pi }{2} - t \Rightarrow dx =  - dt$

Đổi cận:

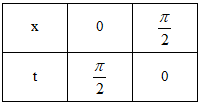
$\begin{array}{l}I = \int\limits_{\frac{\pi }{2}}^0 {\left[ {f\left( t \right) - \sin \left( {\frac{\pi }{2} - t} \right).\cos \left( {\frac{\pi }{2} - t} \right)} \right]\left( { - tdt} \right)} \\ = \int\limits_0^{\frac{\pi }{2}} {\left[ {f\left( t \right) - \sin t.\cos t} \right]dt} \\ = \int\limits_0^{\frac{\pi }{2}} {\left[ {f\left( x \right) - \sin x.\cos x} \right]dx} \\ = \int\limits_0^{\frac{\pi }{2}} { - \sin x.\cos x}  - I =  - \frac{1}{2} - I\\ \Rightarrow I =  - \frac{1}{4}\end{array}$