Câu hỏi:
Cho đồ thị hàm số \(y = f\left( x \right)\). Diện tích \(S\) của hình phẳng (phần tô đậm trong hình vẽ) là
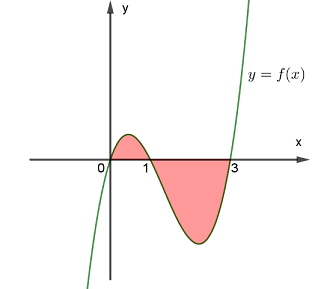
- A \(S = - \int\limits_0^1 {f\left( x \right)dx} + \int\limits_1^3 {f\left( x \right)dx} \)
- B \(S = \int\limits_0^1 {f\left( x \right)dx} - \int\limits_1^3 {f\left( x \right)dx} \)
- C \(S = \int\limits_0^3 {f\left( x \right)dx} \)
- D \(S = \int\limits_0^1 {f\left( x \right)dx} + \int\limits_1^3 {f\left( x \right)dx} \)
Phương pháp giải:
Diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y = f\left( x \right)\), trục hoành và các đường thẳng \(x = a,x = b\) là : \(S = \int\limits_a^b {\left| {f\left( x \right)} \right|dx} \).
Lời giải chi tiết:
Diện tích cần tìm là :
\(\begin{array}{l}S = \int\limits_0^3 {\left| {f\left( x \right)} \right|dx} = \int\limits_0^1 {\left| {f\left( x \right)} \right|dx} + \int\limits_1^3 {\left| {f\left( x \right)} \right|dx} \\\,\,\,\, = \int\limits_0^1 {f\left( x \right)dx} + \int\limits_1^3 {\left( { - f\left( x \right)} \right)dx} \\\,\,\,\, = \int\limits_0^1 {f\left( x \right)dx} - \int\limits_1^3 {f\left( x \right)dx} \end{array}\)
Chọn B.


















