Phương pháp giải:

Chứng minh $AC \bot CD$.

Tìm $\angle SCA \Rightarrow$ quan hệ giữa x và a.

Lời giải chi tiết:

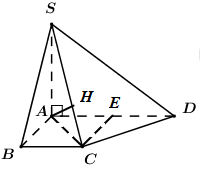
Gọi $E$ là trung điểm của $AD$, ta có $AB = BC = AE = a,\,\,BC\parallel AE,\,\,\angle ABC = {90^0}$ $\Rightarrow ABCE$ là hình vuông.

$\Rightarrow CE = a = \dfrac{1}{2}AD$ $\Rightarrow \Delta ACD$ vuông tại $C$ (định lí đường trung tuyến trong tam giác vuông).

Ta có: $\left\{ \begin{array}{l}CD \bot AC\,\,\left( {cmt} \right)\\CD \bot SA\end{array} \right. \Rightarrow CD \bot \left( {SAC} \right)$

Trong $\left( {SAC} \right)$ kẻ $AH \bot SC\,\,\,\left( {H \in SC} \right)$ ta có: $\left\{ \begin{array}{l}AH \bot CD\\AH \bot SC\end{array} \right. \Rightarrow AH \bot \left( {SCD} \right)$.

$\Rightarrow SH$ là hình chiếu của $SA$ lên $\left( {SCD} \right)$.

$\Rightarrow \angle \left( {SA;\left( {SCD} \right)} \right) = \angle \left( {SA;SH} \right) = \angle ASH = \angle ASC = {30^0}$.

Ta có: $SA \bot \left( {ABCD} \right) \Rightarrow SA \bot AC$ $\Rightarrow \Delta SAC$ vuông tại $A$, có $AC = a\sqrt 2$ (do $ABCE$ là hình vuông cạnh $a$)

$\Rightarrow SA = x = AC.\cot {30^0} = a\sqrt 2 .\sqrt 3  = a\sqrt 6$.

Chọn B.