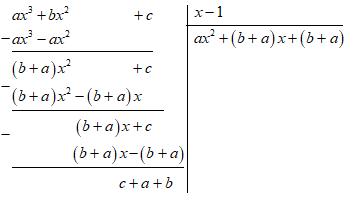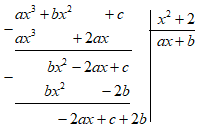Phương pháp giải:

Thực hiện phép chia đa thức một biến đã sắp xếp.

Phép chia hết có dư bằng 0. Từ đó, ta có 1 phương trình.

Phép chia có dư, đồng nhất hệ số với $- 2x + 1$ ta được 2 phương trình.

Giải hệ 3 phương trình 3 ẩn ta được $a,\,\,b,\,\,c.$

Lời giải chi tiết:

Để $a{x^3} + b{x^2} + c$ chia hết cho $x - 1$ thì $a + b + c = 0\,\,\,\,\left( 1 \right)$

Để $a{x^3} + b{x^2} + c$ chia cho ${x^2} + 2$ dư $- 2x + 1$ thì $- 2ax + 2b + c =  - 2x + 1\,$

$\Leftrightarrow \left\{ \begin{array}{l} - 2a =  - 2\\2b + c = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 1\\2b + c = 1\end{array} \right.\,\,\,\left( 2 \right)$

Từ $\left( 1 \right);\,\,\left( 2 \right)$ ta có hệ phương trình:

$\left\{ \begin{array}{l}a = 1\\1 + b + c = 0\\2b + c = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 1\\c =  - 1 - b\\2b - 1 - b = 1\end{array} \right.$ $\Leftrightarrow \left\{ \begin{array}{l}a = 1\\c =  - 1 - b\\b = 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 1\\b = 2\\c =  - 3\end{array} \right.$

Vậy $\left\{ \begin{array}{l}a = 1\\b = 2\\c =  - 3\end{array} \right.$ hay đa thức bị chia là ${x^3} + 2{x^2} - 3.$

Chọn D.