Câu hỏi:
Cho hình lăng trụ đứng \(ABC.A'B'C'\) có đáy là tam giác cân đỉnh \(A\). Biết \(BC = a\sqrt 3 \) và \(\angle ABC = {30^0}\), cạnh bên \(AA' = a\). Gọi \(M\) là điểm thỏa mãn \(2\overrightarrow {CM} = 3\overrightarrow {CC'} \). Gọi \(\alpha \) là góc tạo bởi hai mặt phẳng \(\left( {ABC} \right)\) và \(\left( {AB'M} \right)\), khi đó \(\sin \alpha \) có giá trị bằng:
- A \(\dfrac{{\sqrt {66} }}{{22}}\)
- B \(\dfrac{{\sqrt {481} }}{{22}}\)
- C \(\dfrac{{\sqrt 3 }}{{22}}\)
- D \(\dfrac{{\sqrt {418} }}{{22}}\)
Phương pháp giải:
- Chứng minh \(\angle \left( {\left( {ABC} \right);\left( {AB'M} \right)} \right) = \angle \left( {\left( {B'C'N} \right);\left( {B'MN} \right)} \right)\).
- Trong \(\left( {A'B'C'} \right)\) kẻ \(C'H \bot B'N\), chứng minh \(\angle \left( {\left( {B'C'N} \right);\left( {B'MN} \right)} \right) = \angle \left( {C'H;MH} \right)\).
- Sử dụng diện tích tam giác và định lí Cosin trong tam giác tính \(C'H\).
- Áp dụng tỉ số lượng giác của góc nhọn trong tam giác vuông tính \(\sin \alpha \).
Lời giải chi tiết:
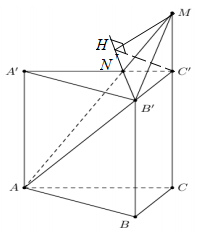
Trong \(\left( {ACC'A'} \right)\) gọi \(N = AM \cap A'C'\) , khi đó ta có \(\left( {AB'M} \right) \equiv \left( {B'MN} \right)\), lại có \(\left( {ABC} \right)\parallel \left( {B'C'N} \right)\).
\( \Rightarrow \angle \left( {\left( {ABC} \right);\left( {AB'M} \right)} \right) = \angle \left( {\left( {B'C'N} \right);\left( {B'MN} \right)} \right)\).
Trong \(\left( {A'B'C'} \right)\) kẻ \(C'H \bot B'N\), ta có: \(\left\{ \begin{array}{l}B'N \bot C'H\\B'N \bot C'M\end{array} \right. \Rightarrow B'N \bot \left( {C'MH} \right) \Rightarrow B'N \bot MH\).
\(\left\{ \begin{array}{l}\left( {B'C'N} \right) \cap \left( {B'MN} \right) = B'N\\C'H \subset \left( {B'C'N} \right),\,\,C'H \bot B'N\\MH \subset \left( {B'MN} \right),\,\,MH \bot B'N\end{array} \right.\)\( \Rightarrow \angle \left( {\left( {B'C'N} \right);\left( {B'MN} \right)} \right) = \angle \left( {C'H;MH} \right) = \angle C'HM = \alpha \).
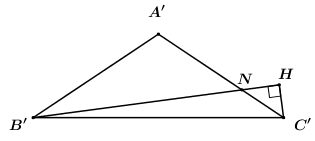
Áp dụng định lí Ta-lét ta có: \(\dfrac{{C'N}}{{AC}} = \dfrac{{MC'}}{{MC}} = \dfrac{1}{3} = \dfrac{{C'N}}{{A'C'}}\).
\( \Rightarrow \dfrac{{{S_{NB'C'}}}}{{{S_{A'B'C'}}}} = \dfrac{{NC'}}{{A'C'}} = \dfrac{1}{3} \Rightarrow {S_{NB'C'}} = \dfrac{1}{3}.{S_{A'B'C'}}\).
Áp dụng định lí Cosin trong tam giác \(A'B'C'\) ta có:
\(\begin{array}{l}\cos \angle A'B'C' = \dfrac{{A'B{'^2} + B'C{'^2} - A'C{'^2}}}{{2A'B'.B'C'}}\\ \Leftrightarrow \cos {30^0} = \dfrac{{3{a^2}}}{{2.A'B'.a\sqrt 3 }}\\ \Leftrightarrow 3a.A'B' = 3{a^2}\\ \Leftrightarrow A'B' = a = A'C',\,\,A'N = \dfrac{2}{3}A'C' = \dfrac{{2a}}{3}\\ \Rightarrow {S_{A'B'C'}} = \dfrac{1}{2}A'B'.A'C'.\sin \angle B'A'C'\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \dfrac{1}{2}.a.a.\sin {120^0} = \dfrac{{{a^2}\sqrt 3 }}{4}\\ \Rightarrow {S_{NB'C'}} = \dfrac{1}{3}{S_{A'B'C'}} = \dfrac{{{a^2}\sqrt 3 }}{{12}}\end{array}\)
Áp dụng định lí Cosin trong tam giác \(A'B'N\) ta có:
\(\begin{array}{l}B'{N^2} = A'B{'^2} + A'{N^2} - 2A'B'.A'N.\cos \angle B'A'N\\B'{N^2} = {a^2} + {\left( {\dfrac{{2a}}{3}} \right)^2} - 2.a.\dfrac{{2a}}{3}.\cos {120^0}\\B'{N^2} = \dfrac{{19{a^2}}}{9} \Rightarrow B'N = \dfrac{{a\sqrt {19} }}{3}\end{array}\)
Lại có \({S_{NB'C'}} = \dfrac{1}{2}C'H.B'N \Rightarrow C'H = \dfrac{{2{S_{NB'C'}}}}{{B'N}} = \dfrac{{a\sqrt {57} }}{{38}}\).
Ta có \(MC' = \dfrac{1}{2}CC' = \dfrac{a}{2}\).
\(MC' \bot \left( {A'B'C'} \right) \Rightarrow MC' \bot C'H \Rightarrow \Delta MC'H\) vuông tại \(C'\).
Áp dụng định lí Pytago ta có: \(MH = \sqrt {MC{'^2} + C'{H^2}} = \sqrt {\dfrac{{{a^2}}}{4} + \dfrac{{3{a^2}}}{{76}}} = \dfrac{{a\sqrt {418} }}{{38}}\).
Vậy \(\sin \alpha = \sin \angle C'HM = \dfrac{{MC'}}{{MH}} = \dfrac{a}{2}:\dfrac{{a\sqrt {418} }}{{38}} = \dfrac{{\sqrt {418} }}{{22}}\).
Chọn D.


















