Phương pháp giải:

- Sử dụng công thức \(\cos \varphi  = \dfrac{{S'}}{S}\), trong đó \(S'\) là hình chiếu vuông góc của \(S\).

- Tính diện tích tam giác \(ABC\), sử dụng công thức \({S_{\Delta ABC}} = \dfrac{1}{2}AB.AC.\sin \angle BAC\).

- Tính độ dài các cạnh của tam giác \(AIB'\), áp dụng định lý Pytago đảo chứng minh \(\Delta AIB'\) vuông.

Lời giải chi tiết:

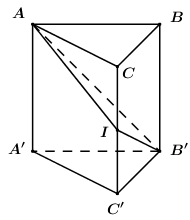
Nhận xét: Hình chiếu vuông góc của tam giác AIB’ lên (ABC) là tam giác ACB.

Khi đó: \(\cos \varphi  = \dfrac{{{S_{ABC}}}}{{{S_{AIB'}}}}\,\,\)với \(\varphi  = \left( {\left( {ABC} \right);\left( {AIB'} \right)} \right)\).

Diện tích tam giác ABC: \({S_{ABC}} = \dfrac{1}{2}AB.AC.\sin A = \dfrac{1}{2}.1.1.\sin {120^0} = \dfrac{{\sqrt 3 }}{4}\)

\(BC = \sqrt {{1^2} + {1^2} - 2.1.1.\cos {{120}^0}}  = \sqrt 3 \)

Tam giác AIB’ có: \(AB' = \sqrt {{1^2} + {1^2}}  = \sqrt 2 \), \(AI = \sqrt {{1^2} + {{\left( {\dfrac{1}{2}} \right)}^2}}  = \dfrac{{\sqrt 5 }}{2}\), \(IB' = \sqrt {{{\left( {\sqrt 3 } \right)}^2} + {{\left( {\dfrac{1}{2}} \right)}^2}}  = \dfrac{{\sqrt {13} }}{2}\)

\( \Rightarrow A{B'^2} + A{I^2} = 2 + \dfrac{5}{4} = \dfrac{{13}}{4} = I{B'^2} \Rightarrow \Delta AIB'\) vuông tại A (Định lí Pytago đảo).

\( \Rightarrow {S_{AIB'}} = \dfrac{1}{2}AB'.AI = \dfrac{1}{2}.\sqrt 2 .\dfrac{{\sqrt 5 }}{2} = \dfrac{{\sqrt {10} }}{4}\).

Vậy \(\cos \varphi  = \dfrac{{{S_{ABC}}}}{{{S_{AIB'}}}}\, = \dfrac{{\dfrac{{\sqrt 3 }}{4}}}{{\dfrac{{\sqrt {10} }}{4}}} = \dfrac{{\sqrt 3 }}{{\sqrt {10} }} = \dfrac{{\sqrt {30} }}{{10}}\).

Chọn D.