Câu hỏi:
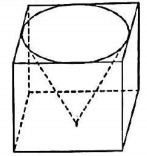
Một khối lập phương có cạnh 1 m chứa đầy nước. Đặt vào trong khối đó 1 khối nón có đỉnh trùng với tâm của một mặt của lập phương, đáy của khối nón tiếp xúc với các cạnh của mặt đối diện. Tính tỉ số thể tích lượng nước trào ra ngoài và thể tích lượng nước ban đầu của khối lập phương.
- A \(\dfrac{4}{\pi }\)
- B \(\dfrac{\pi }{{12}}\)
- C \(\dfrac{{12}}{\pi }\)
- D \(\dfrac{3}{\pi }\)
Phương pháp giải:
- Tính thể tích khối lập phương đã cho.
- Tính thể tích khối nón, từ đó suy ra tỉ lệ thể tích.
Chú ý: Công thức tính thể tích khối lập phương \(V = {a^3}\)
Thể tích khối nón \(V = \dfrac{1}{3}\pi {R^2}h\)
Lời giải chi tiết:
Thể tích khối lập phương \(V = {1^3} = 1\).
Khối nón đã cho có bán kính đáy \(R = \dfrac{1}{2}\), chiều cao \(h = 1\) nên có thể tích:
\({V_n} = \dfrac{1}{3}\pi .{R^2}h = \dfrac{1}{3}\pi .{\left( {\dfrac{1}{2}} \right)^2}.1 = \dfrac{\pi }{{12}}\)
Vậy \(\dfrac{{{V_n}}}{V} = \dfrac{\pi }{{12}}:1 = \dfrac{\pi }{{12}}\).
Chọn B.


















