Câu hỏi:
Cho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác đều cạnh \(a,\)\(SA\) vuông góc với mặt phẳng \(\left( {ABC} \right);\) góc giữa đường thẳng \(SB\) và mặt phẳng \(\left( {ABC} \right)\) bằng \({60^0}.\) Gọi \(M\) là trung điểm của cạnh \(AB.\) Khoảng cách từ \(B\) đến mặt phẳng \(\left( {SMC} \right)\) bằng
- A \(\dfrac{{a\sqrt {39} }}{{13}}.\)
- B \(a\sqrt 3 .\)
- C \(a.\)
- D \(\dfrac{a}{2}.\)
Phương pháp giải:
- Xác định góc giữa \(SB\) và mặt đáy là góc giữa \(SB\) và hình chiếu của \(SB\) lên \(\left( {ABC} \right)\).
- Sử dụng tỉ số lượng giác của tam giác vuông tính \(SA\).
- Đổi \(d\left( {B;\left( {SMC} \right)} \right) = d\left( {A;\left( {SMC} \right)} \right)\).
- Trong \(\left( {SAB} \right)\) kẻ \(AH \bot SM\), chứng minh \(AH \bot \left( {SMC} \right)\).
- Sử dụng hệ thức lượng trong tam giác vuông tính \(AH\).
Lời giải chi tiết:
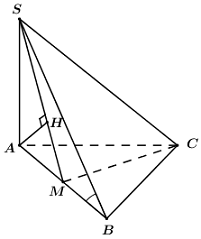
Ta có: \(SA \bot \left( {ABC} \right) \Rightarrow \)\(AB\) là hình chiếu vuông góc của \(SB\) lên \(\left( {ABC} \right)\).
\( \Rightarrow \angle \left( {SB;\left( {ABC} \right)} \right) = \angle \left( {SB;AB} \right) = \angle SBA = {60^0}\).
Tam giác \(SAB\) vuông tại \(A\) \( \Rightarrow SA = AB.\tan \angle SBA = a.\tan {60^0} = a\sqrt 3 \).
Ta có: \(BA \cap \left( {SMC} \right) = M \Rightarrow \dfrac{{d\left( {B;\left( {SMC} \right)} \right)}}{{d\left( {A;\left( {SMC} \right)} \right)}} = \dfrac{{BM}}{{AM}} = 1\).
\( \Rightarrow d\left( {B;\left( {SCM} \right)} \right) = D\left( {A;\left( {SCM} \right)} \right)\)
Trong \(\left( {SAB} \right)\) kẻ \(AH \bot SM\,\,\left( {H \in SM} \right)\) ta có:
\(\left\{ \begin{array}{l}CM \bot AB\\CM \bot SA\end{array} \right. \Rightarrow CM \bot \left( {SAB} \right) \Rightarrow CM \bot AH\)
\(\left\{ \begin{array}{l}AH \bot CM\\AH \bot SM\end{array} \right. \Rightarrow AH \bot \left( {SMC} \right) \Rightarrow d\left( {A;\left( {SMC} \right)} \right) = AH\).
Tam giác \(SAM\) vuông tại \(A\) có \(AH \bot SM\), áp dụng hệ thức lượng ta có:
\( \Rightarrow \dfrac{1}{{A{H^2}}} = \dfrac{1}{{S{A^2}}} + \dfrac{1}{{A{M^2}}} = \dfrac{1}{{{{\left( {a\sqrt 3 } \right)}^2}}} + \dfrac{1}{{{{\left( {\dfrac{a}{2}} \right)}^2}}} = \dfrac{{13}}{{3{a^2}}}\) \( \Rightarrow AH = \dfrac{{\sqrt {39} }}{{13}}a\).
Vậy \(d\left( {B;\left( {SCM} \right)} \right) = \dfrac{{a\sqrt {39} }}{{13}}\).
Chọn A.


















