Câu hỏi:
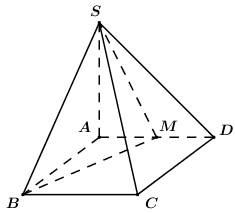
Cho hình chóp \(S.ABCD\) có đáy là hình chữ nhật \(AB = a\), \(AD = 2a\), \(SA\) vuông góc với mặt phẳng đáy và \(SA = a\). Gọi \(M\) là trung điểm của \(AD\). Tính khoảng cách giữa hai đường thẳng \(BM\) và \(SD\).
- A \(\dfrac{{a\sqrt 2 }}{2}\)
- B \(\dfrac{{a\sqrt 6 }}{3}\)
- C \(\dfrac{{a\sqrt 6 }}{6}\)
- D \(\dfrac{{2a\sqrt 5 }}{5}\)
Phương pháp giải:
- Khoảng cách giữa hai đường thẳng chéo nhau là khoảng cách từ đường thẳng này đến mặt phẳng song song và chứa đường thẳng kia, gọi \(N\) là trung điểm của \(BC\), chứng minh \(d\left( {BM;SD} \right) = d\left( {M;\left( {SDN} \right)} \right)\).
- Đổi tính khoảng cách từ \(M\) đến \(\left( {SDN} \right)\) sang tính khoảng cách từ \(A\) đến \(\left( {SDN} \right)\).
- Chứng minh \(DN \bot \left( {SAN} \right)\).
- Trong \(\left( {SAN} \right)\) kẻ \(AH \bot SN\), chứng minh \(AH \bot \left( {SDN} \right)\).
- Sử dụng hệ thức lượng trong tam giác vuông và tính chất tam giác vuông cân để tính khoảng cách.
Lời giải chi tiết:
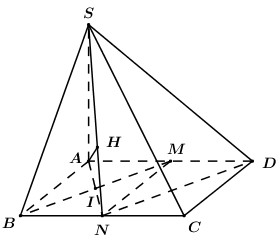
Gọi \(N\) là trung điểm của \(BC\) ta có: \(\left\{ \begin{array}{l}DM = BN\\DM\parallel BN\end{array} \right.\) \( \Rightarrow BNDM\) là hình bình hành \( \Rightarrow BM\parallel DN\).
\( \Rightarrow BM\parallel \left( {SDN} \right) \supset SD\) \( \Rightarrow d\left( {BM;SD} \right) = d\left( {BM;\left( {SDN} \right)} \right) = d\left( {M;\left( {SDN} \right)} \right)\).
Ta có: \(AM \cap \left( {SDN} \right) = D \Rightarrow \dfrac{{d\left( {M;\left( {SDN} \right)} \right)}}{{d\left( {A;\left( {SDN} \right)} \right)}} = \dfrac{{MD}}{{AD}} = \dfrac{1}{2}\) \( \Rightarrow d\left( {M;\left( {SDN} \right)} \right) = \dfrac{1}{2}d\left( {A;\left( {SDN} \right)} \right)\).
Trong \(\left( {ABCD} \right)\) gọi \(I\) là trung điểm của \(BM\).
Ta có \(\left\{ \begin{array}{l}AM = BN\\AM\parallel BN\end{array} \right. \Rightarrow AMNB\) là hình bình hành, do đó hai đường chéo cắt nhau tại trung điểm mỗi đường nên \(I\) cũng là trung điểm của \(AN\), hay \(A,\,\,I,\,\,N\) thẳng hàng.
Xét \(\Delta ABM\) có \(AB = AM = a \Rightarrow \Delta ABM\) vuông cân tại \(A\) \( \Rightarrow AI \bot BM\) \( \Rightarrow AN \bot DN\).
Ta có: \(\left\{ \begin{array}{l}DN \bot AN\\DN \bot SA\end{array} \right. \Rightarrow DN \bot \left( {SAN} \right)\).
Trong \(\left( {SAN} \right)\) kẻ \(AH \bot SN\,\,\left( {H \in SN} \right)\) ta có \(\left\{ \begin{array}{l}AH \bot SN\\AH \bot DN\end{array} \right. \Rightarrow AH \bot \left( {SDN} \right)\) \( \Rightarrow d\left( {A;\left( {SDN} \right)} \right) = AH\).
Tam giác \(ABM\) vuông cân cạnh \(a\) \( \Rightarrow BM = a\sqrt 2 = AN\).
Áp dụng hệ thức lượng trong tam giác vuông \(SAN\) có: \(AH = \dfrac{{SA.AN}}{{\sqrt {S{A^2} + A{N^2}} }} = \dfrac{{a.a\sqrt 2 }}{{\sqrt {{a^2} + 2{a^2}} }} = \dfrac{{a\sqrt 6 }}{3}\).
Vậy \(d\left( {BM;SD} \right) = \dfrac{1}{2}AH = \dfrac{{a\sqrt 6 }}{6}\) .
Chọn C.


















