Phương pháp giải:

- Tìm mối quan hệ giữa \({d_{M;\left( {SBD} \right)}}\) và \({d_{A;\left( {SBD} \right)}}\).

- Tìm khoảng cách từ điểm A xuống mặt phẳng SBD bằng phương pháp 1 nét.

- Sử dụng hệ thức lượng trong tam giác vuông để tính khoảng cách.

Lời giải chi tiết:

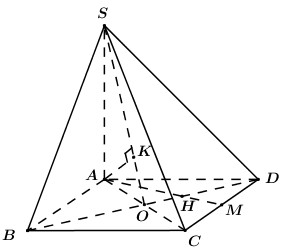
Trong \(\left( {ABCD} \right)\), gọi H là giao điểm của AM và BD.

Ta có: \(MA \cap \left( {SBD} \right) = H\)

 \( \Rightarrow \dfrac{{d\left( {M;\left( {SBD} \right)} \right)}}{{d\left( {A;\left( {SBD} \right)} \right)}} = \dfrac{{MH}}{{AH}} = \dfrac{{DM}}{{AB}} = \dfrac{1}{2}\)  (Định lí Ta-lét).

\( \Rightarrow d\left( {M;\left( {SBD} \right)} \right) = \dfrac{1}{2}d\left( {A;\left( {SBD} \right)} \right)\)

Gọi O là tâm hình vuông ABCD , trong \(\left( {SAO} \right)\) ker \(AK \bot SO\,\,\left( {K \in SO} \right)\) ta có:

\(\begin{array}{l}\left\{ \begin{array}{l}BD \bot AO\\BD \bot SA\end{array} \right. \Rightarrow SD \bot \left( {SAO} \right) \Rightarrow BD \bot AK\\\left\{ \begin{array}{l}AK \bot BD\\AK \bot SO\end{array} \right. \Rightarrow AK \bot \left( {SBD} \right)\\ \Rightarrow d\left( {A;\left( {SBD} \right)} \right) = AK\end{array}\)

Do \(ABCD\) là hình vuông cạnh \(a\) nên \(AC = a\sqrt 2  \Rightarrow AO = \dfrac{1}{2}AC = \dfrac{{a\sqrt 2 }}{2}\).

Áp dụng hệ thức lượng trong tam giác vuông \(SAO\) có: \(AK = \dfrac{{SA.AO}}{{\sqrt {S{A^2} + A{O^2}} }} = \dfrac{{2a.\dfrac{{a\sqrt 2 }}{2}}}{{\sqrt {4{a^2} + \dfrac{{{a^2}}}{2}} }} = \dfrac{{2a}}{3}\).

Vậy  \(d\left( {M;\left( {SBD} \right)} \right) = \dfrac{1}{2}AK = \dfrac{a}{3}\).

Chọn D.