Phương pháp giải:

Áp dụng định lý Pitago cho các tam giác vuông để tính cạnh của hình lập phương.

Thể tích khối lập phương cạnh $a$ là: $V = {a^3}.$

Lời giải chi tiết:

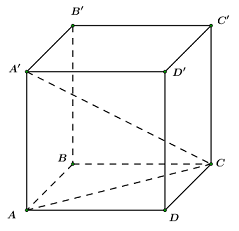
Gọi cạnh của hình lập phương là $a.$

Áp dụng định lý Pitago cho $\Delta ABC$ vuông tại $A$ ta có: $A{C^2} = A{D^2} + A{B^2} = {a^2} + {a^2} = 2{a^2}.$

Áp dụng định lý Pitago cho $\Delta AA'C$ vuông tại $A$ ta có: $A'{C^2} = A{C^2} + AA{'^2} = 2{a^2} + {a^2} = 3{a^2}$

$\begin{array}{l} \Rightarrow 3{a^2} = 1 \Leftrightarrow {a^2} = \dfrac{1}{3} \Leftrightarrow a = \dfrac{1}{{\sqrt 3 }}.\\ \Rightarrow V = {\left( {\dfrac{1}{{\sqrt 3 }}} \right)^3} = \dfrac{1}{{3\sqrt 3 }}.\end{array}$

Chọn A.