Câu hỏi:
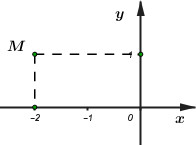
Trong mặt phẳng tọa độ, cho điểm MM như hình vẽ bên là điểm biểu diễn số phức zz. Tính (z+1)2.(z+1)2.
- A (1+z)2=−2i.(1+z)2=−2i.
- B (1+z)2=−8i.(1+z)2=−8i.
- C (1+z)2=−1+i.(1+z)2=−1+i.
- D (1+z)2=−2+2i.(1+z)2=−2+2i.
Phương pháp giải:
Cho số phức z=a+bi(a,b∈R)⇒M(a;b) là điểm biểu diễn số phức z.
Lời giải chi tiết:
Dựa vào đồ thị hàm số ta thấy điểm M(−2;1)⇒z=−2+i.
⇒(1+z)2=(1−2+i)2=(i−1)2=i2−2i+1=−2i.
Chọn A.
Quảng cáo
Câu hỏi trước
