Câu hỏi:
Trên một sợi dây đàn hồi căng ngang có ba điểm A, B và C sao cho AB = 1cm, BC = 7cm. Khi sóng dừng hình thành trên sợi dây với bước sóng \(\lambda = 12cm\)và tần số f = 50Hz thì A là một nút sóng, B và C cùng dao động điều hòa theo phương thẳng đứng. Gọi d1 và d2 lần lượt là khoảng cách lớn nhất giữa A với B, và khoảng cách lớn nhất giữa A với C. Biết biên độ của điểm bụng là \({a_B} = 2cm\), tỉ số \(\dfrac{{{d_2}}}{{{d_1}}}\) bằng
- A 2
- B \(2\sqrt 5 \)
- C 5,8
- D 4
Phương pháp giải:
+ Công thức tính biên độ: \(a = {A_B}.\left| {\sin \dfrac{{2\pi d}}{\lambda }} \right|\)
Trong đó d là khoảng cách từ điểm ta xét đến nút sóng.
+ Áp dụng định lí Pitago.
Lời giải chi tiết:
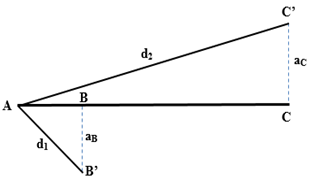
Biên độ của sóng tại B và C:
\(\left\{ \begin{array}{l}{a_B} = {A_B}.\left| {\sin \dfrac{{2\pi .AB}}{\lambda }} \right| = 2.\left| {\sin \dfrac{{2\pi .1}}{{12}}} \right| = 1cm\\{a_C} = {A_B}.\left| {\sin \dfrac{{2\pi .AC}}{\lambda }} \right| = 2.\left| {\sin \dfrac{{2\pi .8}}{{12}}} \right| = \sqrt 3 cm\end{array} \right.\)
Ta có: \(\left\{ \begin{array}{l}{d_1} = \sqrt {A{B^2} + a_B^2} = \sqrt {{1^2} + {1^2}} = \sqrt 2 cm\\{d_2} = \sqrt {A{C^2} + a_C^2} = \sqrt {{8^2} + {{\left( {\sqrt 3 } \right)}^2}} = \sqrt {67} cm\end{array} \right. \Rightarrow \dfrac{{{d_2}}}{{{d_1}}} = 5,8\)
Chọn C.


















