Câu hỏi:
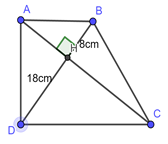
Cho hình thang vuông \(ABCD\,\,\,\,\left( {\angle A = \angle D = {{90}^0}} \right)\) có hai đường chéo \(AC\) và \(BD\) vuông góc với nhau tại \(H.\) Biết \(HD = 18cm,\,\,HB = 8cm,\) tính diện tích hình thang \(ABCD\).
- A \(504cm^2\)
- B \(505cm^2\)
- C \(506cm^2\)
- D \(507cm^2\)
Phương pháp giải:
Sử dụng hệ thức lượng trong tam giác vuông và công thức tính diện tích hình thang có hai đường chéo vuông góc.
Lời giải chi tiết:
Xét \(\Delta ADB\) vuông tại \(A\) có:
\(AH\) là đường cao ứng với cạnh huyền \(BD\)
\( \Rightarrow H{A^2} = HB.HD = 8.18 \Rightarrow HA = 12\left( {cm} \right)\) (hệ thức lượng trong tam giác vuông)
Xét \(\Delta ADC\) vuông tại \(D\) có:
\(DH\) là đường cao ứng với cạnh huyền \(AC\)
\( \Rightarrow H{D^2} = HA.HC \Rightarrow {18^2} = 12HC\)\( \Rightarrow HC = 27\left( {cm} \right)\) (hệ thức lượng trong tam giác vuông)
Ta có: \(AC = AH + HC = 12 + 27 = 39\,\,cm.\)
\(BD = BH + HD = 8 + 18 = 26\,\,cm.\)
\( \Rightarrow {S_{ABCD}} = \frac{{AC.BD}}{2} = \frac{{26.39}}{2} = 507\,\,c{m^2}.\)
Chọn D.