Câu hỏi:
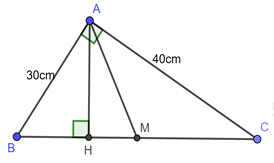
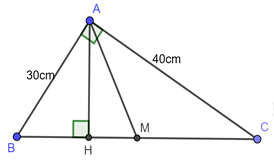
Cho tam giác \(ABC\) vuông tại \(A\) có cạnh \(AB = 30cm\) và \(AC = 40cm\), đường cao \(AH\), trung tuyến \(AM\).
Câu 1:
Tính \(BH,\,\,HM,\,\,MC.\)
- A \(BH = 18cm\,\,;\,\,\,HM = 7cm\,\,;\,\,\,MC = 25cm\)
- B \(BH = 12cm\,\,;\,\,\,HM = 8cm\,\,;\,\,\,MC = 20cm\)
- C \(BH = 16cm\,\,;\,\,\,HM = 8cm\,\,;\,\,\,MC = 24cm\)
- D \(BH = 16cm\,\,;\,\,\,HM = 6cm\,\,;\,\,\,MC = 22cm\)
Phương pháp giải:
Sử dụng định lý Pitago, hệ thức lượng trong tam giác vuông và tính chất đường trung tuyến của tam giác để tính các cạnh tương ứng.
Lời giải chi tiết:
Áp dụng định lý Pitago cho \(\Delta ABH\) vuông tại \(A\) có: \(A{B^2} + A{C^2} = B{C^2}\)
\( \Leftrightarrow B{C^2} = {30^2} + {40^2} = 2500 \Rightarrow BC = 50\,\,cm.\)
Áp dụng hệ thức lượng trong \(\Delta ABC\) vuông tại \(A\) có đường cao \(AH\) ta có:
\(A{B^2} = BH.BC\) \( \Leftrightarrow {30^2} = 50.BH \Leftrightarrow BH = 18\,\,cm.\)
Vì \(AM\) là đường trung tuyến \( \Rightarrow M\) là trung điểm \(BC\)\( \Rightarrow BM = MC = \frac{1}{2}BC = \frac{1}{2}.50 = 25\,\,cm.\)
Ta có: \(MH = BM - BH = 25 - 18 = 7\,\,cm.\)
Chọn A.
Câu 2:
Tính \(AH.\)
- A \(AH = 18cm\)
- B \(AH = 22cm\)
- C \(AH = 24cm\)
- D \(AH = 28cm\)
Phương pháp giải:
Sử dụng hệ thức lượng: \(AH.BC = AB.AC.\)
Lời giải chi tiết:
Áp dụng hệ thức lượng trong \(\Delta ABC\) vuông tại \(A\) có đường cao \(AH\) ta có:
\(AH.BC = AB.AC\)\( \Leftrightarrow AH.50 = 30.40 \Leftrightarrow AH = 24\,\,cm.\)
Chọn C.