Phương pháp giải:

- Chứng minh \(SM \bot \left( {ABCD} \right)\).

- Sử dụng định lí: \(AB\parallel \left( P \right) \Rightarrow d\left( {A;\left( P \right)} \right) = d\left( {B;\left( P \right)} \right)\), đổi đỉnh tính khoảng cách từ M đến (SCD).

- Gọi N là trung điểm của CD, trong (SMN) dựng \(MH \bot SN\), chứng minh \(MH \bot \left( {SCD} \right)\).

- Đặt \(AB = x\), tính MC, MD theo x.

- Xác định góc giữa SC và (ABCD) là góc giữa SC và hình chiếu của SC lên (ABCD), từ đó tính SM theo x.

- Áp dụng định lí Pytago trong tam giác vuông SMD tìm x, từ đó tính được SM và MN theo a.

- Áp dụng hệ thức lượng trong tam giác vuông để tính khoảng cách.

Lời giải chi tiết:

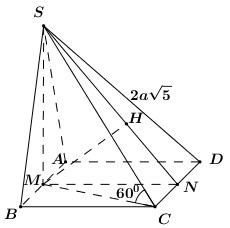
Vì tam giác SAB cân tại S nên \(SM \bot AB\).

Ta có: \(\left\{ \begin{array}{l}\left( {SAB} \right) \bot \left( {ABCD} \right)\\\left( {SAB} \right) \cap \left( {ABCD} \right) = AB\\SM \subset \left( {SAB} \right),\,\,SM \bot AB\end{array} \right.\) \( \Rightarrow SM \bot \left( {ABCD} \right)\).

\( \Rightarrow MC\) là hình chiếu của SC lên (ABCD) \( \Rightarrow \angle \left( {SC;\left( {ABCD} \right)} \right) = \angle \left( {SC;MC} \right) = \angle SCM = {60^0}\).

Gọi N là trung điểm của CD \( \Rightarrow MN \bot CD\).

Trong (SMN) kẻ \(MH \bot SN\,\,\left( {H \in SN} \right)\).

Ta có: \(\left\{ \begin{array}{l}CD \bot MN\\CD \bot SM\,\,\left( {SM \bot \left( {ABCD} \right)} \right)\end{array} \right.\) \( \Rightarrow CD \bot \left( {SMN} \right) \Rightarrow CD \bot MH\).

\(\left\{ \begin{array}{l}MH \bot CD\\MH \bot SN\end{array} \right. \Rightarrow MH \bot \left( {SCD} \right)\) \( \Rightarrow d\left( {M;\left( {SCD} \right)} \right) = MH\).

Ta có: \(AM\parallel CD \Rightarrow AM\parallel \left( {SCD} \right)\), do đó \(d\left( {A;\left( {SCD} \right)} \right) = d\left( {M;\left( {SCD} \right)} \right) = MH\).

Gọi cạnh của hình vuông ABCD bằng x.

Áp dụng định lí Pytago ta có: \(MC = MD = \sqrt {{x^2} + \dfrac{{{x^2}}}{4}}  = \dfrac{{x\sqrt 5 }}{2}\).

Xét tam giác vuông SMC có: \(SM = MC.\tan {60^0} = \dfrac{{x\sqrt {15} }}{2}\).

Áp dụng định lí Pytago trong tam giác vuông SMD có:

\(\begin{array}{l}S{M^2} + M{D^2} = S{D^2}\\ \Leftrightarrow \dfrac{{15{x^2}}}{4} + \dfrac{{5{x^2}}}{4} = 20{a^2}\\ \Leftrightarrow 5{x^2} = 20{a^2}\\ \Leftrightarrow {x^2} = 4{a^2} \Leftrightarrow x = 2a\end{array}\)

\( \Rightarrow MN = x = 2a\) và \(SM = \dfrac{{2a.\sqrt {15} }}{2} = a\sqrt {15} \).

Áp dụng hệ thức lượng trong tam giác vuông SMN có:

\(\dfrac{1}{{M{H^2}}} = \dfrac{1}{{S{M^2}}} + \dfrac{1}{{M{N^2}}} = \dfrac{1}{{15{a^2}}} + \dfrac{1}{{4{a^2}}} = \dfrac{{19}}{{60{a^2}}}\) \( \Rightarrow MH = \dfrac{{2a\sqrt {285} }}{{19}}\).

Vậy \(d\left( {A;\left( {SCD} \right)} \right) = \dfrac{{2a\sqrt {285} }}{{19}} = \dfrac{{2a\sqrt {15} }}{{\sqrt {19} }}\).

Chọn C.