Phương pháp giải:

Lời giải chi tiết:

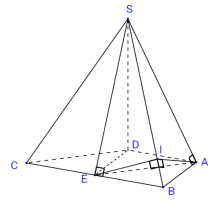
Tam giác \(SBC\) cân tại \(S\) có \(BC = 4a\). Gọi \(E\) là trung điểm của \(BC\) \( \Rightarrow SE \bot BC\) (trung tuyến đồng thời là đường cao) và \(BE = \dfrac{1}{2}BC = 2a = BA\).

Trong \(\left( {SAB} \right)\) kẻ \(AI \bot SB\,\,\left( {I \in SB} \right)\).

Xét \(\Delta SAB\) và \(\Delta SEB\) có:

\(\begin{array}{l}\angle SAB = \angle SEB = {90^0}\\SB\,\,chung\\AB = EB = 2a\,\,\left( {cmt} \right)\end{array}\)

\( \Rightarrow \Delta SAB = \Delta SEB\) (cạnh huyền – cạnh góc vuông).

\( \Rightarrow \angle SBA = \angle SBE\).

Xét \(\Delta ABI\) và \(\Delta EBI\) có:

\(\begin{array}{l}AB = EB = 2a\\\angle SBA = \angle SBE\,\,\left( {cmt} \right)\\BI\,\,chung\end{array}\)

\( \Rightarrow \Delta ABI = \Delta EBI\,\,\left( {c.g.c} \right) \Rightarrow \angle AIB = \angle EIB = {90^0}\), suy ra \(EI \bot SB\) và \(AI = EI\).

Ta có: \(\left( {SBC} \right) \equiv \left( {SBE} \right)\).

\(\left\{ \begin{array}{l}\left( {SBE} \right) \cap \left( {SAB} \right) = SB\\\left( {SBE} \right) \supset EI \bot SB\\\left( {SAB} \right) \supset AI \bot SB\end{array} \right.\)\( \Rightarrow \angle \left( {\left( {SBE} \right);\left( {SAB} \right)} \right) = \angle \left( {AI;EI} \right) = {60^0}\).

Áp dụng định lí Pytago trong tam giác vuông \(ABE\) ta có: \(AE = \sqrt {A{B^2} + B{E^2}}  = 2a\sqrt 2 \).

TH1: \(\angle AIE = {60^0}\).

Áp dụng định lí Cosin trong tam giác \(AIE\) ta có:

\(\begin{array}{l}\cos \angle AIE = \dfrac{{A{I^2} + E{I^2} - A{E^2}}}{{2AI.EI}}\\ \Leftrightarrow \dfrac{1}{2} = \dfrac{{2A{I^2} - 8{a^2}}}{{2A{I^2}}}\\ \Leftrightarrow 2A{I^2} = 4A{I^2} - 16{a^2}\\ \Leftrightarrow A{I^2} = 8{a^2} \Leftrightarrow AI = 2a\sqrt 2  > AB\,\,\left( {ktm} \right)\end{array}\)

TH2: \(\angle AIE = {120^0}\)

Áp dụng định lí Cosin trong tam giác \(AIE\) ta có:

\(\begin{array}{l}\cos \angle AIE = \dfrac{{A{I^2} + E{I^2} - A{E^2}}}{{2AI.EI}}\\ \Leftrightarrow  - \dfrac{1}{2} = \dfrac{{2A{I^2} - 8{a^2}}}{{2A{I^2}}}\\ \Leftrightarrow  - 2A{I^2} = 4A{I^2} - 16{a^2}\\ \Leftrightarrow A{I^2} = \dfrac{{8{a^2}}}{3} \Leftrightarrow AI = \dfrac{{2a\sqrt 2 }}{{\sqrt 3 }}\end{array}\)

Ta có:

\(\begin{array}{l}{V_{S.ABE}} = {V_{S.AIE}} + {V_{B.AIE}} = \dfrac{1}{3}SI.{S_{\Delta AIE}} + \dfrac{1}{3}BI.{S_{\Delta AIE}}\\\,\,\,\,\,\,\,\,\,\,\,\,\, = \dfrac{1}{3}{S_{\Delta AIE}}.\left( {SI + BI} \right) = \dfrac{1}{3}{S_{\Delta AIE}}.SB\end{array}\)

Áp dụng định lí Pytago trong tam giác vuông \(ABI\) ta có: \(BI = \sqrt {A{B^2} - A{I^2}}  = \dfrac{{2a\sqrt 3 }}{3}\).

Áp dụng hệ thức lượng trong tam giác vuông \(SAB\) ta có: \(SB = \dfrac{{A{B^2}}}{{BI}} = 2a\sqrt 3 \).

Ta có \({S_{\Delta AIE}} = \dfrac{1}{2}AI.EI.sin\angle AIE = \dfrac{1}{2}.\dfrac{{8{a^2}}}{3}.\dfrac{{\sqrt 3 }}{2} = \dfrac{{2{a^2}\sqrt 3 }}{3}\).

Vậy \({V_{S.ABE}} = \dfrac{1}{3}.\dfrac{{2{a^2}\sqrt 3 }}{3}.2a\sqrt 3  = \dfrac{{4{a^3}}}{3}\).

Mà \({S_{ABC}} = 2{S_{ABE}}\) nên \({V_{S.ABC}} = 2{V_{S.ABE}} = \dfrac{{8{a^3}}}{3}\).

Chọn B.