Phương pháp giải:

Lời giải chi tiết:

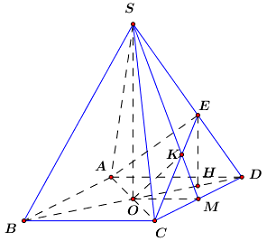
Gọi \(O = AC \cap BD\), vì chóp \(S.ABCD\) đều \( \Rightarrow SO \bot \left( {ABCD} \right)\).

Gọi \(M\) là trung điểm của \(CD\), ta có: \(\left\{ \begin{array}{l}CD \bot OM\\CD \bot SO\end{array} \right.\)

\( \Rightarrow CD \bot \left( {SOM} \right)\).

Trong \(\left( {SOM} \right)\) kẻ \(OK \bot SM\,\,\left( {K \in SM} \right)\) ta có:

\(\left\{ \begin{array}{l}OK \bot SM\\OK \bot CD\end{array} \right.\) \( \Rightarrow OK \bot \left( {SCD} \right)\).

Mà \(O \in \left( P \right) \Rightarrow OK \subset \left( P \right) \Rightarrow K \in \left( P \right)\).

Trong \(\left( {SCD} \right)\) gọi \(E = CK \cap SD \Rightarrow E = \left( P \right) \cap SD\). Khi đó \(\left( P \right) \equiv \left( {ACE} \right)\).

Trong \(\left( {SBD} \right)\) kẻ \(EH\parallel SO\,\,\left( {H \in BD} \right)\), suy ra \(EH \bot \left( {ABCD} \right)\).

Ta có: \(\dfrac{{{V_1}}}{V} = \dfrac{{{V_{D.ACE}}}}{{{V_{S.ABCD}}}} = \dfrac{{\dfrac{1}{3}EH.{S_{ACD}}}}{{\dfrac{1}{3}SO.{S_{ABCD}}}} = \dfrac{{EH}}{{SO}}.\dfrac{1}{2}\) \( \Rightarrow \dfrac{1}{5} = \dfrac{{EH}}{{SO}}.\dfrac{1}{2} \Rightarrow \dfrac{{EH}}{{SO}} = \dfrac{2}{5} = \dfrac{{DE}}{{DS}}\)

Ta có: \(\left\{ \begin{array}{l}\left( {SCD} \right) \cap \left( {ABCD} \right) = CD\\\left( {SCD} \right) \supset SM \bot CD\\\left( {ABCD} \right) \supset OM \bot CD\end{array} \right.\)\( \Rightarrow \angle \left( {\left( {SCD} \right);\left( {ABCD} \right)} \right) = \angle \left( {SM;OM} \right) = \angle SMO\).

Áp dụng định lí Menelaus trong tam giác \(SMD\) có:

\(\dfrac{{KS}}{{KM}}.\dfrac{{CM}}{{CD}}.\dfrac{{ED}}{{ES}} = 1\)\( \Leftrightarrow \dfrac{{KS}}{{KM}}.\dfrac{1}{2}.\dfrac{2}{3} = 1 \Leftrightarrow \dfrac{{KS}}{{KM}} = 3\)\( \Rightarrow \dfrac{{MK}}{{MS}} = \dfrac{1}{4}\).

Áp dụng hệ thức lượng trong tam giác vuông \(SOM\), đường cao \(OK\) ta có:

\(O{M^2} = MK.MS \Rightarrow \dfrac{{O{M^2}}}{{M{S^2}}} = \dfrac{{MK}}{{MS}} = \dfrac{1}{4}\) \( \Rightarrow \dfrac{{OM}}{{MS}} = \dfrac{1}{2} = \cos \angle SMO\). 

Chọn A.