Phương pháp giải:

- Xác định góc giữa hai mặt phẳng là góc giữa hai đường thẳng lần lượt thuộc hai mặt phẳng và cùng vuông góc với giao tuyến.

- Áp dụng định lí Cô-sin trong tam giác: \(\cos A = \dfrac{{{b^2} + {c^2} - {a^2}}}{{2bc}}\).

Lời giải chi tiết:

Tam giác \(ABC,\,\,ABD\) là các tam giác cân tại \(C\) và \(D\) nên \(CM \bot AB,\,\,DM \bot AB\).

Ta có: \(\left\{ \begin{array}{l}\left( {ABC} \right) \cap \left( {ABD} \right) = AB\\\left( {ABC} \right) \supset CM \bot AB\\\left( {ABD} \right) \supset DM \bot AB\end{array} \right.\) \( \Rightarrow \angle \left( {\left( {ABC} \right);\left( {ABD} \right)} \right) = \angle \left( {CM;DM} \right) = \alpha \).

Gọi \(I\) là trung điểm của MN.

Kẻ \(IK \bot AD\) mà mặt cầu đường kính \(MN\) tiếp xúc với \(AD \Rightarrow IK = IM = IN\).

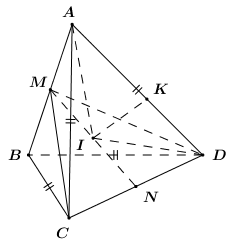
Xét \(\Delta AMI\) và \(\Delta AKI\) có:

\(\begin{array}{l}\angle AMI = \angle AKI = {90^0}\\AI\,\,chung\\IM = IK\,\,\left( {cmt} \right)\end{array}\)

\( \Rightarrow \Delta AMI = \Delta AKI\) (cạnh huyền – cạnh góc vuông).

\( \Rightarrow AM = AK = \dfrac{a}{2}\).

\( \Rightarrow DK = AD - AK = \dfrac{{a\sqrt 3 }}{2} - \dfrac{a}{2} = \dfrac{{a\left( {\sqrt 3  - 1} \right)}}{2}\).

Chứng minh tương tự ta có \(DK = DN \Rightarrow DN = \dfrac{{a\left( {\sqrt 3  - 1} \right)}}{2}\) \( \Rightarrow CD = a\left( {\sqrt 3  - 1} \right)\).

Ta có: \(CM \bot AB\) nên \(\Delta ACM\) vuông tại \(M\), áp dụng định lí Pytago ta có:

\(CM = \sqrt {A{C^2} - A{M^2}}  = \sqrt {\dfrac{{3{a^2}}}{4} - \dfrac{{{a^2}}}{4}}  = \dfrac{{a\sqrt 2 }}{2}\).

Tương tự ta tính được \(DM = \dfrac{{a\sqrt 2 }}{2}\).

Áp dụng định lí Cô-sin trong tam giác \(MCD\) có:

\(\begin{array}{l}{\rm{cos}}\angle CMD = \dfrac{{M{C^2} + M{D^2} - C{D^2}}}{{2.MC.MD}}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \dfrac{{\dfrac{{{a^2}}}{2} + \dfrac{{{a^2}}}{2} - {a^2}{{\left( {\sqrt 3  - 1} \right)}^2}}}{{2.\dfrac{{{a^2}}}{2}}} = 2\sqrt 3  - 3 > 0\end{array}\)

Vậy \(\cos \alpha  = \cos \angle CMD = 2\sqrt 3  - 3\).

Chọn B.