Phương pháp giải:

- Hình chiếu của đỉnh xuống mặt đáy của hình chóp đều là tâm của đáy.

- Tìm góc tạo bởi giữa mặt đáy và mặt bên.

- Tìm góc giữa hai mặt phẳng \(\left( {SAB} \right)\) và \(\left( {SAC} \right)\).

- Sử dụng giả thiết khoảng cách từ \(H\) đến \(SA\) bằng \(\dfrac{a}{{\sqrt 7 }}\) để tìm các cạnh của hình chóp và giải bài toán.

Lời giải chi tiết:

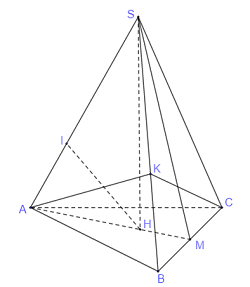
Vì \(S.ABC\)là hình chóp đều nên \(\left\{ \begin{array}{l}SA = SB = SC\\AB = AC = BC\end{array} \right.\) và \(H\) là tâm của mặt đáy \(ABC\).

Gọi \(M\) là trung điểm của \(BC\).

Tam giác \(ABC\) là tam giác đều nên \(AM \bot BC\) và \(AH = \dfrac{2}{3}AM\).

Tam giác \(SBC\) cân tại \(S\) nên \(SM \bot BC\)

Ta có:

\(\left\{ \begin{array}{l}\left( {SBC} \right) \cap \left( {ABC} \right) = BC\\SM \subset \left( {SBC} \right),\,\,SM \bot BC\\AM \subset \left( {ABC} \right),\,\,AM \bot BC\end{array} \right.\)\( \Rightarrow \widehat {\left( {SBC} \right),\left( {ABC} \right)} = \widehat {SMA} \Rightarrow \widehat {SMA} = 60^\circ \) 

Qua \(H,\) kẻ \(HI \bot SA\,\left( {I \in SA} \right)\), từ giả thiết suy ra \(HI = \dfrac{a}{{\sqrt 7 }}\)

Tam giác \(SHM\) vuông tại \(H\) nên \(\tan SMH = \dfrac{{SH}}{{HM}} \Rightarrow \dfrac{{SH}}{{HM}} = \sqrt 3  \Rightarrow SH = \sqrt 3 HM = \dfrac{{\sqrt 3 }}{2}AH\)

Tam giác \(SHA\) vuông tại \(H\) có \(HI \bot SA\) nên ta có:

      \(\dfrac{1}{{H{I^2}}} = \dfrac{1}{{S{H^2}}} + \dfrac{1}{{A{H^2}}} \Leftrightarrow \dfrac{1}{{\dfrac{{{a^2}}}{7}}} = \dfrac{1}{{\dfrac{3}{4}A{H^2}}} + \dfrac{1}{{A{H^2}}} \Leftrightarrow \dfrac{7}{{{a^2}}} = \dfrac{7}{{3A{H^2}}} \Rightarrow \left\{ \begin{array}{l}AH = \dfrac{{\sqrt 3 }}{3}a\\SH = \dfrac{a}{2}\end{array} \right.\)

Qua \(A,\) kẻ \(AK \bot SB\left( {K \in SB} \right)\,\,\,\,\left( 1 \right)\).

Ta có:\(\left\{ \begin{array}{l}BH \bot AC\\SH \bot \left( {ABC} \right) \Rightarrow SH \bot AC\end{array} \right.\)\( \Rightarrow AC \bot \left( {SBH} \right) \Rightarrow AC \bot SB\,\,\,\,\,\left( 2 \right)\) 

Từ (1) và (2) suy ra \(SB \bot \left( {AKC} \right) \Rightarrow SB \bot KC\).

Do đó, góc giữa hai mặt phẳng \(\left( {SAB} \right)\) và \(\left( {SAC} \right)\) cũng là góc giữa hai mặt phẳng \(\left( {SAB} \right)\) và \(\left( {SBC} \right)\) và là góc giữa hai đường thẳng \(AK\) và \(KC\).

Ta có:

\(\begin{array}{l}SA = SB = SC = \sqrt {A{H^2} + S{H^2}}  = \dfrac{{\sqrt {21} a}}{6}\\AB = AC = BC = \dfrac{2}{{\sqrt 3 }}AM = \dfrac{2}{{\sqrt 3 }}.\dfrac{3}{2}AH = a\end{array}\)

\( \Rightarrow {S_{\Delta SAB}} = \dfrac{{\sqrt 3 }}{6}{a^2} \Rightarrow AK = KC = \dfrac{{2{S_{\Delta SAB}}}}{{SB}} = \dfrac{{2\sqrt 7 a}}{7}\)

Do đó, \(\cos AKC = \dfrac{{A{K^2} + K{C^2} - A{C^2}}}{{2AK.KC}} = \dfrac{1}{8} \Rightarrow \cos \alpha  = \dfrac{1}{8}\)

Suy ra \(\tan \dfrac{\alpha }{2} = \dfrac{{\sqrt 7 }}{3}\).

Chọn A.