Câu hỏi:
Cho hình chóp \(S.ABC\) có đáy là tam giác vuông cân ở đỉnh C và \(SA \bot \left( {ABC} \right),SC = a\). Gọi \(x\) là góc giữa hai mặt phẳng \(\left( {SCB} \right)\) và \(\left( {ABC} \right)\) để thể tích khối chóp \(S.ABC\) lớn nhất. Giá trị \(\cos x\) bằng
- A \(0\)
- B \(1\)
- C \(\sqrt {\dfrac{2}{3}} \)
- D \(\sqrt {\dfrac{1}{3}} \)
Phương pháp giải:
- Góc giữa hai mặt phẳng là góc giữa hai đường thẳng lần lượt thuộc hai mặt phẳng và cùng vuông góc với giao tuyến, từ đó xác định góc \(x\).
- Tính \(SA;\,\,\,{S_{ABC}}\) theo \(x\).
- Tính thể tích khối chóp \({V_{S.ABC}} = \dfrac{1}{3}SA.{S_{ABC}}\).
- Sử dụng phương pháp hàm số xác định giá trị lớn nhất của hàm thể tích.
Lời giải chi tiết:
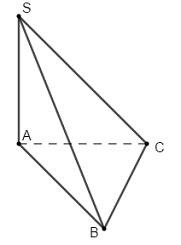
Ta có \(\left\{ \begin{array}{l}BC \bot AC\\BC \bot SA\end{array} \right. \Rightarrow BC \bot \left( {SAC} \right)\)\( \Rightarrow BC \bot SC.\)
Khi đó ta có: \(\left\{ \begin{array}{l}\left( {SBC} \right) \cap \left( {ABC} \right) = BC\\\left( {SBC} \right) \supset SC \bot BC\\\left( {ABC} \right) \supset AC \bot BC\end{array} \right.\)
\( \Rightarrow \angle \left( {\left( {SBC} \right);\left( {ABC} \right)} \right) = \angle \left( {SC;AC} \right) = \angle SCA\).
\( \Rightarrow x = \angle SCA\).
Ta có: \(SA \bot \left( {ABC} \right) \Rightarrow SA \bot AC\) \( \Rightarrow \Delta SAC\) vuông tại \(A\).
Tam giác \(SAC\) vuông tại A có \(SC = a;\,\,\angle SCA = x\)\( \Rightarrow \left\{ \begin{array}{l}SA = a.\sin x\\AC = BC = a.\cos x\end{array} \right.\)
\( \Rightarrow {S_{\Delta ABC}} = \dfrac{1}{2}AC.BC = \dfrac{1}{2}{a^2}{\cos ^2}x\).
\(\begin{array}{l} \Rightarrow V = \dfrac{1}{3}.SA.{S_{ABC}} = \dfrac{1}{3}.{a^3}.\sin x.\dfrac{1}{2}{a^2}{\cos ^2}x\\ \Rightarrow V = \dfrac{1}{6}{a^3}\sin x{\cos ^2}x = \dfrac{{{a^3}}}{6}\sin x\left( {1 - {{\sin }^2}x} \right)\\ \Rightarrow V = \dfrac{{{a^3}}}{6}\left( {\sin x - {{\sin }^3}x} \right)\end{array}\)
Xét hàm số \(f\left( x \right) = \sin x - {\sin ^3}x\) với \(x \in \left( {0;\dfrac{\pi }{2}} \right]\). Đặt \(t = \sin x\), \(t \in \left( {0;1} \right]\).
Khi đó hàm số trở thành: \(f\left( t \right) = t - {t^3}\) với \(t \in \left( {0;1} \right]\).
Ta có: \(f'\left( t \right) = 1 - 3{t^2} = 0 \Leftrightarrow t = \dfrac{1}{{\sqrt 3 }}\).
BBT:
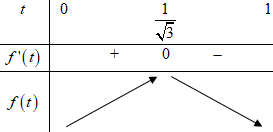
Dựa vào BBT ta thấy hàm số \(y = f\left( t \right)\) đạt giá trị lớn nhất \( \Leftrightarrow t = \dfrac{1}{{\sqrt 3 }}\).
Khi đó thể tích khối chóp đạt GTLN tại \(\sin x = \dfrac{1}{{\sqrt 3 }}\) \( \Leftrightarrow \cos x = \sqrt {1 - {{\sin }^2}x} = \sqrt {\dfrac{2}{3}} \).
Chọn C.


















