Phương pháp giải:

Sử dụng công thức tính khoảng cách dựa vào thể tích: $d\left( {A;\left( {SBC} \right)} \right) = \dfrac{{3{V_{S.ABC}}}}{{{S_{\Delta SBC}}}}$.

Lời giải chi tiết:

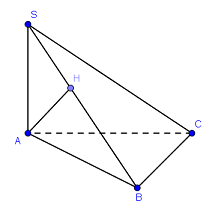
Ta có: $\left\{ \begin{array}{l}BC \bot AB\,\,\left( {gt} \right)\\BC \bot SA\,\,\left( {SA \bot \left( {ABC} \right)} \right)\end{array} \right.$$\Rightarrow BC \bot \left( {SAB} \right).$

$\Rightarrow BC \bot SB$$\Rightarrow {S_{SBC}} = \dfrac{1}{2}.SB.BC = \dfrac{1}{2}.2a.a = {a^2}.$

$d\left( {A;\left( {SBC} \right)} \right) = \dfrac{{3{V_{S.ABC}}}}{{{S_{\Delta SBC}}}} = \dfrac{{3{a^3}}}{{{a^2}}} = 3a.$

Chọn: A.