Câu hỏi:
Cho tam giác ABC có trọng tâm G. Gọi H là điểm đối xứng của B qua G. Đẳng thức nào sau đây đúng?
- A \(\overrightarrow {AH} = - {1 \over 3}\overrightarrow {AB} + {2 \over 3}\overrightarrow {AC} \)
- B \(\overrightarrow {AH} = - {1 \over 2}\overrightarrow {AB} + {1 \over 3}\overrightarrow {AC} \)
- C \(\overrightarrow {AH} = - {1 \over 4}\overrightarrow {AB} + {1 \over 3}\overrightarrow {AC} \)
- D \(\overrightarrow {AH} = {1 \over 3}\overrightarrow {AB} + {2 \over 3}\overrightarrow {AC} \)
Lời giải chi tiết:
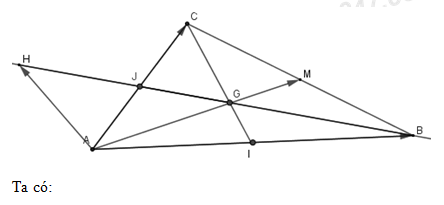
\(\eqalign{& \,\,\,\,\,\overrightarrow {AH} = \overrightarrow {AG} + \overrightarrow {GH} = {2 \over 3}\overrightarrow {AM} + \overrightarrow {BG} \cr & = {2 \over 3}\left( {{{\overrightarrow {AB} + \overrightarrow {AC} } \over 2}} \right) + {2 \over 3}\overrightarrow {BJ} \cr & = {1 \over 3}\overrightarrow {AB} + {1 \over 3}\overrightarrow {AC} + {2 \over 3}\left( {{{\overrightarrow {BC} + \overrightarrow {BA} } \over 2}} \right) \cr & = {1 \over 3}\overrightarrow {AB} + {1 \over 3}\overrightarrow {AC} + {1 \over 3}\overrightarrow {BC} - {1 \over 3}\overrightarrow {AB} \cr & = {1 \over 3}\overrightarrow {AC} + {1 \over 3}\overrightarrow {BA} + {1 \over 3}\overrightarrow {AC} \cr & = {2 \over 3}\overrightarrow {AC} - {1 \over 3}\overrightarrow {AB} \cr} \)
Chọn A.


















