Câu hỏi:
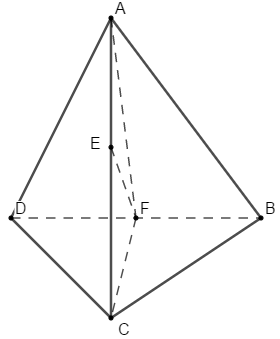
Xét tứ diện \(ABCD\) có \(AB = BC = CD = DA = 1\) và \(AC,\,\,BD\) thay đổi. Giá trị lớn nhất của thể tích khối tứ diện \(ABCD\) bằng
- A \(\frac{{2\sqrt 3 }}{{27}}.\)
- B \(\frac{{4\sqrt 3 }}{{27}}.\)
- C \(\frac{{2\sqrt 3 }}{9}.\)
- D \(\frac{{4\sqrt 3 }}{9}.\)
Phương pháp giải:
Sử dụng công thức tính thể tích và đặt \(AC = x,\,\,\,BD = y.\) Từ đó sử dụng bất đẳng thức để đánh giá và tìm giá trị lớn nhất của thể tích tứ diện cần tìm.
Lời giải chi tiết:
Đặt \(AC = x,\,\,\,BD = y.\)
Gọi \(E,\,\,\,F\) lần lượt là trung điểm của \(AC,\,\,\,BD.\)
\(\begin{array}{l} \Rightarrow \left\{ \begin{array}{l}FA \bot BD\\CF \bot BD\end{array} \right. \Leftrightarrow BD \bot \left( {ACF} \right)\\ \Rightarrow BD \bot AC;\,\,FE \bot AC\\ \Rightarrow AC \bot \left( {BED} \right)\end{array}\)
Mặt khác:
\(\begin{array}{l}{V_{ABCD}} = 2{V_{ABDE}} = \frac{2}{3}.AE.{S_{BED}} = \frac{2}{3}.AE.FE.BF\\ \Rightarrow {V_{ABCD}} = \frac{2}{3}.\frac{x}{2}.\frac{y}{2}.FE\end{array}\)
Mà \(F{E^2} = B{E^2} - B{F^2} = 1 - \frac{{{x^2}}}{4} - \frac{{{y^2}}}{4}\)
\( \Leftrightarrow {V^2} = \frac{1}{{144}}.{x^2}{y^2}\left( {4 - {x^2} - {y^2}} \right) \le \frac{1}{{144}}{\left( {\frac{{{x^2} + {y^2} + \left( {4 - {x^2} - {y^2}} \right)}}{3}} \right)^3} = \frac{4}{{243}}\)
Dấu bằng xảy ra khi \({x^2} = {y^2} = 4 - {x^2} - {y^2} \Leftrightarrow x = y = \frac{{2\sqrt 3 }}{3}\)
\( \Rightarrow {V_{{\rm{max}}}} = \frac{{2\sqrt 3 }}{{27}}.\)
Chọn A.