Phương pháp giải:

Lời giải chi tiết:

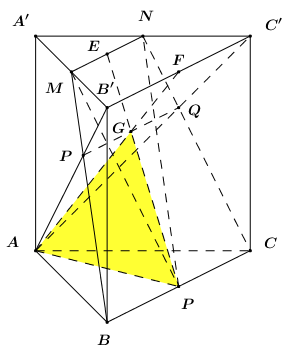
Ta có \(\left( {MNP} \right) \equiv \left( {MNCB} \right)\).

Gọi \(E,\,\,F\) lần lượt là trung điểm của \(MN,\,\,B'C'\).

Dễ dàng chứng minh được \(\Delta AA'B' = \Delta AA'C'\) (hai cạnh góc vuông)

\( \Rightarrow AB' = AC' \Rightarrow \Delta AB'C'\) cân tại \(A\).

\( \Rightarrow AF \bot B'C'\) (Đường trung tuyến đồng thời là đường cao).

Ta có \(MN\parallel B'C' \Rightarrow MN\parallel BC\) nên \(MNCB\) là hình thang.

Dễ dàng chứng minh được \(\Delta BB'M = \Delta CC'N\) nên \(BM = CN\).

Mà \(BM,\,\,CN,\,\,AA'\) đồng quy (Định lí 3 đường giao tuyến) nên \(MNCB\) là hình thang cân.

Lại có \(E,\,\,P\) là trung điểm của hai đáy nên \(EP \bot MN,\,\,EP \bot BC\).

Trong \(\left( {ACC'A'} \right)\) gọi \(Q = CN \cap AC'\), trong \(\left( {ABB'A'} \right)\) gọi \(P = AB' \cap BM\).

Khi đó \(\left( {AB'C'} \right) \cap \left( {MNCB} \right) = PQ\).

Ta có: \(\left\{ \begin{array}{l}\left( {AB'C'} \right) \supset B'C'\\\left( {MNCB} \right) \supset BC\\B'C'\parallel BC\end{array} \right.\) \( \Rightarrow \left( {AB'C'} \right) \cap \left( {MNCB} \right) = PQ\parallel BC\parallel MN\).

Do đó \(PQ \bot EP\).

Ta có: \(\left\{ \begin{array}{l}\left( {MNCB} \right) \cap \left( {AB'C'} \right) = PQ\\\left( {MNCB} \right) \supset EP \bot PQ\\\left( {AB'C'} \right) \supset AF \bot PQ\end{array} \right.\) \( \Rightarrow \angle \left( {\left( {MNCB} \right);\left( {AB'C'} \right)} \right) = \angle \left( {EP;AF} \right)\)

Trong \(\left( {AB'C'} \right)\) gọi \(G = PQ \cap AF\).

Áp dụng định lí Ta-lét ta có: \(\dfrac{{AQ}}{{QC'}} = \dfrac{{AC}}{{NC'}} = 2 \Rightarrow \dfrac{{AQ}}{{AC'}} = \dfrac{2}{3}\); \(\dfrac{{AG}}{{AF}} = \dfrac{{AQ}}{{AC'}} = \dfrac{2}{3}\).

Áp dụng định lí Pytago trong các tam giác vuông ta có:

\(AB' = \sqrt {AA{'^2} + A'B{'^2}}  = \sqrt {4 + 12}  = 4\);

\(AF = \sqrt {AB{'^2} - B'{F^2}}  = \sqrt {16 - 3}  = \sqrt {13} \).

\( \Rightarrow AG = \dfrac{2}{3}AF = \dfrac{{2\sqrt {13} }}{3}\).

Gọi \(H,\,\,K\) lần lượt là hình chiếu của \(M,\,\,N\) trên \(BC\), ta có \(BH = KC = \dfrac{{BC - MN}}{2} = \dfrac{{2\sqrt 3  - \sqrt 3 }}{2} = \dfrac{{\sqrt 3 }}{2}\).

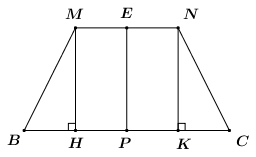
Áp dụng định lí Pytago trong các tam giác vuông ta có:

\(BM = \sqrt {BB{'^2} + B'{M^2}}  = \sqrt {4 + 3}  = \sqrt 7 \).

\(MH = \sqrt {B{M^2} - B{H^2}}  = \sqrt {7 - \dfrac{3}{4}}  = \dfrac{5}{2} = EP\).

Áp dụng định lí Ta-lét ta có: \(\dfrac{{GP}}{{GE}} = \dfrac{{AP}}{{EF}} = 2\) \( \Rightarrow GP = \dfrac{2}{3}EP = \dfrac{5}{3}\).

Tam giác \(ABC\) đều cạnh \(2\sqrt 3 \) nên \(AP = \dfrac{{2\sqrt 3 .\sqrt 3 }}{2} = 3\).

Áp dụng định lí Côsin trong tam giác \(AGP\) ta có:

\(\cos \angle AGP = \dfrac{{G{A^2} + G{P^2} - A{P^2}}}{{2GA.GP}} = \dfrac{{{{\left( {\dfrac{{2\sqrt {13} }}{3}} \right)}^2} + {{\left( {\dfrac{5}{3}} \right)}^2} - {3^2}}}{{2.\dfrac{{2\sqrt {13} }}{3}.\dfrac{5}{3}}} =  - \dfrac{{\sqrt {13} }}{{65}}\).

Vậy \(\cos \angle \left( {\left( {MNCB} \right);\left( {AB'C'} \right)} \right) = \cos \angle \left( {EP;AF} \right) = \dfrac{{\sqrt {13} }}{{65}}\).

Chọn B.