Phương pháp giải:

Lời giải chi tiết:

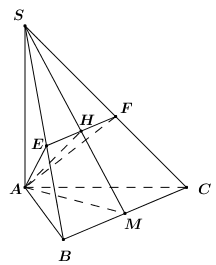
Trong \(\left( {SAM} \right)\) kẻ \(AH \bot SM \Rightarrow AH \subset \left( \alpha  \right)\).

Trong \(\left( {SBC} \right)\) kẻ \(EF\) đi qua \(H\) và \(EF \bot SM\) \(\left( {E \in SB,\,\,F \in SC} \right)\), suy ra \(EF \subset \left( \alpha  \right)\).

\( \Rightarrow \left( \alpha  \right) \equiv \left( {AEF} \right)\).

Xét \({\Delta _v}SAB\) và \({\Delta _v}SAC\) có:

\(\begin{array}{l}SA\,\,chung\\AB = AC\,\,\,\left( {gt} \right)\end{array}\)

\( \Rightarrow {\Delta _v}SAB = {\Delta _v}SAC\) (cạnh huyền – cạnh góc vuông)

\( \Rightarrow SB = SC \Rightarrow \Delta SBC\) cân tại \(S\), do đó \(SM \bot BC\).

Mà \(SM \bot EF \Rightarrow EF\parallel BC\). Áp dụng định lí Ta-lét ta có: \(\dfrac{{SE}}{{SB}} = \dfrac{{SF}}{{SC}}\).

Ta có: \(\dfrac{{{V_{S.AEF}}}}{{{V_{S.ABC}}}} = \dfrac{{SE}}{{SB}}.\dfrac{{SF}}{{SC}} = {\left( {\dfrac{{SE}}{{SB}}} \right)^2} = \dfrac{1}{4}\) \( \Rightarrow \dfrac{{SE}}{{SB}} = \dfrac{1}{2} = \dfrac{{SF}}{{SC}} = \dfrac{{SH}}{{SM}} \Rightarrow \)\(H\) là trung điểm của \(SM\).

Xét tam giác \(SAM\) vuông tại \(A\) có đường cao \(AH\) đồng thời là trung tuyến.

\( \Rightarrow \Delta SAM\) vuông cân tại \(A\) \( \Rightarrow SA = AM = \dfrac{{a\sqrt 3 }}{2}\).

\(\Delta ABC\) đều cạnh \(a\) nên \({S_{\Delta ABC}} = \dfrac{{{a^2}\sqrt 3 }}{4}\).

Vậy \({V_{S.ABC}} = \dfrac{1}{3}SA.{S_{\Delta ABC}}\) \( = \dfrac{1}{3}.\dfrac{{a\sqrt 3 }}{2}\dfrac{{{a^2}\sqrt 3 }}{4} = \dfrac{{{a^3}}}{8}\).

Chọn B.