Phương pháp giải:

Sử dụng phương pháp tọa độ trong không gian.

Lời giải chi tiết:

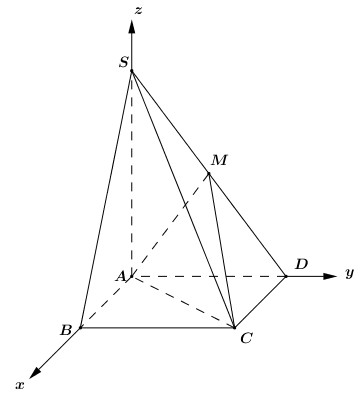
Đặt \(A\left( {0;0;0} \right)\), \(S\left( {0;0;x} \right)\), \(D\left( {0;1;0} \right)\), \(B\left( {1;0;0} \right)\), \(C\left( {1;1;0} \right)\)\( \Rightarrow M\left( {0;\dfrac{1}{2};\dfrac{x}{2}} \right)\).

\( \Rightarrow \left\{ \begin{array}{l}\overrightarrow {AM} \left( {0;\dfrac{1}{2};\dfrac{x}{2}} \right)\\\overrightarrow {AC} \left( {1;1;0} \right)\end{array} \right.\)\( \Rightarrow {\overrightarrow n _{\left( {AMC} \right)}} = \left[ {\overrightarrow {AM} ;\overrightarrow {AC} } \right] = \left( { - \dfrac{x}{2};\dfrac{x}{2}; - \dfrac{1}{2}} \right)\)

    \(\left\{ \begin{array}{l}\overrightarrow {SB} \left( {1;0; - x} \right)\\\overrightarrow {BC} \left( {0;1;0} \right)\end{array} \right.\)\( \Rightarrow {\overrightarrow n _{\left( {SBC} \right)}} = \left[ {\overrightarrow {SB} ;\overrightarrow {BC} } \right] = \left( {x;0;1} \right)\) .

Ta có: \(\tan \varphi  = \dfrac{{2\sqrt 5 }}{5}\)\( \Rightarrow \cos \varphi  = \dfrac{1}{{\sqrt {1 + {{\tan }^2}\varphi } }} = \dfrac{{\sqrt 5 }}{3}\)  

\(\begin{array}{l} \Rightarrow \cos \left( \varphi  \right) = \dfrac{{\left| {{{\overrightarrow n }_{\left( {AMC} \right)}}.{{\overrightarrow n }_{\left( {SBC} \right)}}} \right|}}{{\left| {{{\overrightarrow n }_{\left( {AMC} \right)}}} \right|.\left| {{{\overrightarrow n }_{\left( {SBC} \right)}}} \right|}} = \dfrac{{\sqrt 5 }}{3}\\ \Rightarrow \dfrac{{\left| {\dfrac{{ - {x^2}}}{2} - \dfrac{1}{2}} \right|}}{{\sqrt {\dfrac{{{x^2}}}{2} + \dfrac{1}{4}} .\sqrt {{x^2} + 1} }} = \dfrac{{\sqrt 5 }}{3}\\ \Leftrightarrow \dfrac{{\dfrac{{{x^2} + 1}}{2}}}{{\dfrac{{\sqrt {2{x^2} + 1} .\sqrt {{x^2} + 1} }}{2}}} = \dfrac{{\sqrt 5 }}{3}\\ \Leftrightarrow \dfrac{{\sqrt {{x^2} + 1} }}{{\sqrt {2{x^2} + 1} }} = \dfrac{{\sqrt 5 }}{3} \Leftrightarrow 9\left( {{x^2} + 1} \right) = 5\left( {2{x^2} + 1} \right)\\ \Leftrightarrow {x^2} = 4 \Leftrightarrow x = 2 \Rightarrow SA = 2a\end{array}\)

Ta có: \({V_{SABCM}} = {V_{SABCD}} - {V_{SMACD}}\).

\(\dfrac{{{V_{MACD}}}}{{{V_{S.ABCD}}}} = \dfrac{{d\left( {M;\left( {ABCD} \right)} \right)}}{{d\left( {S;\left( {ABCD} \right)} \right)}}.\dfrac{{{S_{ACD}}}}{{{S_{ABCD}}}} = \dfrac{1}{4}\).

\( \Rightarrow {V_{SABCM}} = \dfrac{3}{4}{V_{S.ABCD}}\) \( = \dfrac{3}{4}.\dfrac{1}{3}.2a.{a^2} = \dfrac{{{a^3}}}{2}\).

Chọn C.