Câu hỏi:
Cho hình lăng trụ tam giác đều \(ABC.A'B'C'\) có tất cả các cạnh bằng \(a\). Gọi \(M,\,\,N\) lần lượt là trung điểm của các cạnh \(AB,\,\,B'C'\). Mặt phẳng \(\left( {A'MN} \right)\) cắt cạnh \(BC\) tại \(P\). Thể tích của khối đa diện \(MBP.A'B'N\) bằng:
- A \(\dfrac{{7\sqrt 3 {a^3}}}{{32}}.\)
- B \(\dfrac{{7\sqrt 3 {a^3}}}{{96}}.\)
- C \(\dfrac{{\sqrt 3 {a^3}}}{{24}}.\)
- D \(\dfrac{{\sqrt 3 {a^3}}}{{12}}.\)
Phương pháp giải:
Sử dụng tỉ số thể tích.
Lời giải chi tiết:
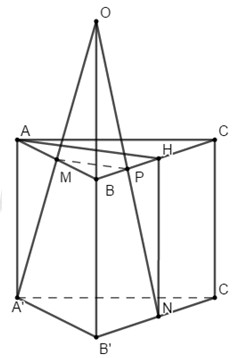
Trong \(\left( {ABB'A'} \right)\) gọi \(A'M \cap BB' = O\).
Trong mặt phẳng \(\left( {BCC'B'} \right)\) nối \(NO\) cắt \(BC\) tại \(P\).
Áp dụng định lí Ta-lét ta có:
\(\dfrac{{OM}}{{OA'}} = \dfrac{{OB}}{{OB'}} = \dfrac{{OP}}{{ON}} = \dfrac{{BM}}{{A'B'}} = \dfrac{1}{2}\).
\(\begin{array}{l} \Rightarrow \dfrac{{{V_{O.MBP}}}}{{{V_{O.A'B'N}}}} = \dfrac{{OM}}{{OA'}}.\dfrac{{OB}}{{OB'}}.\dfrac{{OP}}{{ON}} = \dfrac{1}{8}\\ \Rightarrow {V_{MBP.A'B'N}} = \dfrac{7}{8}.{V_{O.A'B'N}}\end{array}\)
Lại có
\(\begin{array}{l}{V_{OA'B'N}} = \dfrac{1}{3}.OB.{S_{A'B'N}}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \dfrac{1}{3}OB.\dfrac{1}{2}A'B'.B'N.\sin {60^0}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \dfrac{1}{6}.2a.a.\dfrac{a}{2}.\dfrac{{\sqrt 3 }}{2} = \dfrac{{{a^3}\sqrt 3 }}{{12}}\end{array}\)
Vậy \({V_{MBP.A'B'N}} = \dfrac{7}{8}.\dfrac{{{a^3}\sqrt 3 }}{{12}} = \dfrac{{7{a^3}\sqrt 3 }}{{96}}\).
Chọn B.


















