 Môn Toán - Lớp 12
Môn Toán - Lớp 12
 40 bài tập trắc nghiệm giá trị lớn nhất, giá trị nhỏ nhất của hàm số mức độ vận dụng, vận dụng cao
40 bài tập trắc nghiệm giá trị lớn nhất, giá trị nhỏ nhất của hàm số mức độ vận dụng, vận dụng cao
Câu hỏi:
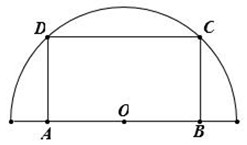
Diện tích lớn nhất của hình chữ nhật \(ABCD\) nội tiếp trong nửa đường tròn (tham khảo hình vẽ) có bán kính bằng \(10\,\,cm\) là:
- A \(100 \,\,c{m^2}.\)
- B \(160 \,\,c{m^2}.\)
- C \(80 \,\,c{m^2}.\)
- D \(200 \,\,c{m^2}.\)
Phương pháp giải:
- Đặt \(OA = x\), tính \(AD\) theo \(x\) và tính diện tích hình chữ nhật \(ABCD\).
- Sử dụng phương pháp hàm số tìm GTLN.
Lời giải chi tiết:
Đặt \(OA = x\,\,\left( {0 < x < 10} \right) \Rightarrow AB = 2x.\)
Áp dụng định lí Pytago trong tam giác vuông \(OAD\) ta có: \(AD = \sqrt {100 - {x^2}} \).
Khi đó \({S_{ABCD}} = AB.AD = 2x\sqrt {100 - {x^2}} \).
Ta có: \(S' = 2\sqrt {100 - {x^2}} + \dfrac{{ - 4{x^2}}}{{2\sqrt {100 - {x^2}} }} = 0\)
\( \Leftrightarrow 4\left( {100 - {x^2}} \right) - 4{x^2} = 0\)\( \Leftrightarrow {x^2} = 50\)\( \Leftrightarrow x = 5\sqrt 2 \,\,\left( {tm} \right)\).
Vậy \({S_{\max }} = S\left( {5\sqrt 2 } \right) = 100\,\,c{m^2}.\)
Chọn A.

















