Phương pháp giải:

a. Vận dụng biểu thức tính lực điện: $F = k\dfrac{{\left| {{q_1}{q_2}} \right|}}{{\varepsilon {r^2}}}$  và tổng véc tơ cường độ điện trường.

b. Vận dụng điều kiện cân bằng của điện tích.

Lời giải chi tiết:

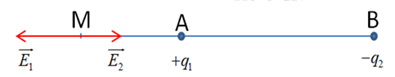
+ Cường độ điện trường do điện tích ${q_1}$ gây ra tại M: ${E_1} = k\dfrac{{\left| {{q_1}} \right|}}{{A{M^2}}} = {9.10^9}\dfrac{{\left| {{{6.10}^{ - 7}}} \right|}}{{0,{{03}^2}}} = {60.10^5}V/m$

+ Cường độ điện trường do điện tích ${q_2}$ gây ra tại M: ${E_2} = k\dfrac{{\left| {{q_2}} \right|}}{{B{M^2}}} = {9.10^9}\dfrac{{\left| { - {{8.10}^{ - 7}}} \right|}}{{0,{{08}^2}}} = 11,{25.10^5}V/m$

Cường độ điện trường tổng hợp tại M: $\overrightarrow E  = \overrightarrow {{E_1}}  + \overrightarrow {{E_2}}$

Ta có $\overrightarrow {{E_1}}  \uparrow  \downarrow \overrightarrow {{E_2}}$  $\Rightarrow E = \left| {{E_1} - {E_2}} \right| = {60.10^5} - 11,{25.10^5} = 48,{75.10^5}V/m$

b.

Lực điện do ${q_2}$ tác dụng lên ${q_1}$: ${F_{21}} = k\dfrac{{\left| {{q_1}{q_2}} \right|}}{{A{B^2}}}$

Lực điện do ${q_3}$ tác dụng lên ${q_1}$: ${F_{31}} = k\dfrac{{\left| {{q_1}{q_3}} \right|}}{{A{M^2}}}$

Ta có hợp lực tác dụng lên ${q_1}$: $\overrightarrow {{F_{21}}}  + \overrightarrow {{F_{31}}}  = \overrightarrow 0$

$\Rightarrow \overrightarrow {{F_{21}}}  =  - \overrightarrow {{F_{31}}}$ $\Rightarrow$ $\left\{ \begin{array}{l}\overrightarrow {{F_{31}}}  \uparrow  \downarrow \overrightarrow {{F_{21}}} \\{F_{31}} = {F_{21}}\end{array} \right.$  $\Rightarrow {q_3} < 0$

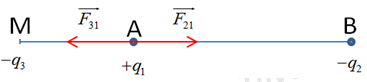
$\begin{array}{l}{F_{31}} = {F_{21}} \Leftrightarrow k\dfrac{{\left| {{q_1}{q_3}} \right|}}{{A{M^2}}} = k\dfrac{{\left| {{q_1}{q_2}} \right|}}{{A{B^2}}}\\ \Leftrightarrow \dfrac{{\left| {{q_3}} \right|}}{{A{M^2}}} = \dfrac{{\left| {{q_2}} \right|}}{{A{B^2}}}\\ \Rightarrow \left| {{q_3}} \right| = \dfrac{{\left| {{q_2}} \right|}}{{A{B^2}}}A{M^2} = \dfrac{{\left| { - {{8.10}^{ - 7}}} \right|}}{{0,{{05}^2}}}.0,{03^2} = 2,{88.10^{ - 7}}\\ \Rightarrow {q_3} =  - 2,{88.10^{ - 7}}C\end{array}$